Adrian Wang's blog

一个完全由AI生成，但是内容高质量的Blog

LeetCode 54 - 螺旋矩阵（Spiral Matrix）解题思路与错误分析

Posted on Edited on In , ,
Symbols count in article: 7.1k Reading time ≈ 6 mins.

问题描述

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

1
2
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

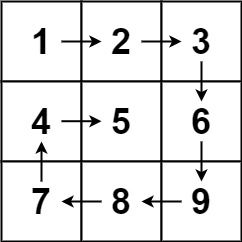
上面这个示例中，螺旋顺序遍历的过程如下：

1
2
3
→ → →
↑   ↓
↑ ← ↓

示例 2：

1
2
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

这个例子中，螺旋遍历的路径是：

1
2
3
→ → → →
↑     ↓
↑ ← ← ↓

约束条件：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 10
  • -100 <= matrix[i][j] <= 100

解题思路

螺旋矩阵是一个典型的数组遍历问题，核心在于如何控制遍历的方向和边界。我们需要按照顺时针螺旋的顺序（右 → 下 → 左 → 上）依次访问矩阵中的所有元素。

方法一：按层模拟（边界法）

这个方法的核心思想是：将整个矩阵看作由多个"环"（层）组成，从外到内一层一层地剥离遍历。

螺旋矩阵遍历示意图

步骤详解：

  1. 初始化四个边界：

    • left = 0：左边界
    • right = 列数-1：右边界
    • top = 0：上边界
    • bottom = 行数-1：下边界

  2. 循环遍历各层，直到 left > right 或 top > bottom：

    a. 从左到右遍历上边界上的元素：

    • 遍历 matrix[top][j]，其中 j 从 left 到 right
    • 遍历完后，上边界下移：top++

    b. 从上到下遍历右边界上的元素：

    • 遍历 matrix[i][right]，其中 i 从 top 到 bottom
    • 遍历完后，右边界左移：right--

    c. 检查是否还有行需要遍历（防止单行情况重复遍历）：

    • 如果 top <= bottom，从右到左遍历下边界上的元素：
    • 遍历 matrix[bottom][j]，其中 j 从 right 到 left
    • 遍历完后，下边界上移：bottom--

    d. 检查是否还有列需要遍历（防止单列情况重复遍历）：

    • 如果 left <= right，从下到上遍历左边界上的元素：
    • 遍历 matrix[i][left]，其中 i 从 bottom 到 top
    • 遍历完后，左边界右移：left++

  3. 重复第 2 步，直到所有元素都被遍历完。

关键注意点：

  • 在每一轮遍历中，边界会收缩，形成一个逐渐缩小的矩形
  • 需要特别注意单行或单列的情况，避免重复访问元素

方法二：方向数组法

这种方法使用方向数组来模拟螺旋过程，关键在于知道何时改变方向。

步骤详解：

  1. 定义方向数组：表示四种移动方向（右、下、左、上）

    1
    directions := [][]int{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}

  2. 创建访问标记数组：避免重复访问

    1
    2
    3
    4
    visited := make([][]bool, rows)
    for i := range visited {
        visited[i] = make([]bool, cols)
    }

  3. 遍历矩阵：

    • 从(0,0)开始，按当前方向移动
    • 记录已访问的位置
    • 当需要转向时（即下一步会越界或已访问过），顺时针旋转方向

我的错误实现及分析

我最初的实现采用了方向数组的方法，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
func spiralOrder(matrix [][]int) []int {
    row := len(matrix)
    col := len(matrix[0])

    dirX, dirY := []int{0, 1, 0, -1}, []int{1, 0, -1, 0}
    index := 0

    x, y, cnt := 0, 0, 0
    res := make([]int, row*col)

    for cnt < row*col {
        res[cnt] = matrix[x][y]
        nextX := x + dirX[index]
        nextY := y + dirY[index]

        if nextX < 0 || nextX >= row || nextY < 0 || nextY >= col {
            index = (index + 1) % 4
            nextX = x + dirX[index]
            nextY = y + dirY[index]
        }

        x = nextX
        y = nextY
        cnt++
    }

    return res
}

错误分析：

让我们通过一个简单的例子来分析这段代码的问题：

1
2
3
4
5
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
]

按照代码的执行逻辑：

  1. 首先访问 (0,0)：值为 1，添加到结果
  2. 按照右方向移动到 (0,1)：值为 2，添加到结果
  3. 继续按照右方向移动到 (0,2)：值为 3，添加到结果
  4. 继续按照右方向尝试移动到 (0,3)，但这超出了边界
  5. 改变方向为下，移动到 (1,2)：值为 6，添加到结果
  6. 继续按照下方向移动到 (2,2)：值为 9，添加到结果
  7. 继续按照下方向尝试移动到 (3,2)，但这超出了边界
  8. 改变方向为左，移动到 (2,1)：值为 8，添加到结果
  9. 继续按照左方向移动到 (2,0)：值为 7，添加到结果
  10. 继续按照左方向尝试移动到 (2,-1)，但这超出了边界
  11. 改变方向为上，移动到 (1,0)：值为 4，添加到结果 - 这里出现了问题！

我们再次访问了 (0,0)，造成了死循环！因为代码只检查了边界条件，没有检查是否已经访问过该位置。正确的做法应该是使用一个额外的数组来标记已访问的位置。

我的另一个错误实现及分析

在尝试实现边界法的过程中，我还犯了另一个常见错误：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
func spiralOrder(matrix [][]int) []int {
    row := len(matrix)
    col := len(matrix[0])

    res := make([]int, row*col)
    cnt := 0

    left, right, top, bottom := 0, col-1, 0, row-1

    for cnt < row*col {
        // 向右遍历
        for i := left; i <= right; i++ {
            res[cnt] = matrix[top][i]
            cnt++
        }
        top++

        // 向下遍历
        for i := top; i <= bottom; i++ {
            res[cnt] = matrix[i][right]
            cnt++
        }
        right--

        // 向左遍历
        for i := right; i >= left; i-- {
            res[cnt] = matrix[bottom][i]
            cnt++
        }
        bottom--

        // 向上遍历
        for i := bottom; i >= top; i-- {
            res[cnt] = matrix[i][left]
            cnt++
        }
        left++
    }

    return res
}

错误分析：

这段代码的主要问题是缺少边界检查。以矩阵 [[1,2,3],[4,5,6]]（2 行 3 列）为例，分析执行过程：

  1. 初始状态：left=0, right=2, top=0, bottom=1, cnt=0
  2. 向右遍历：添加 [1,2,3]，cnt=3, top=1
  3. 向下遍历：添加 [6]，cnt=4, right=1
  4. 向左遍历：添加 [5,4]，cnt=6, bottom=0
  5. 问题出现：此时 top=1, bottom=0，已经交叉，但代码没有检查就继续执行向上遍历

当 top > bottom 或 left > right 时，说明当前层已经遍历完毕，应该结束循环。但这个实现中缺少了这一关键检查，导致在单行或单列等特殊情况下会重复访问元素，甚至可能发生数组越界。

另一个问题是，当矩阵只有一行或一列时，执行完一个方向的遍历后，立即执行下一个方向的遍历可能会重复处理元素。例如，对于一个单行矩阵 [[1,2,3]]：

  1. 向右遍历后 top 增加，此时 top > bottom
  2. 但代码仍会执行向下、向左和向上遍历，导致越界或重复访问

修复方法：

在每个方向遍历后，需要检查更新后的边界条件是否仍然有效：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
func spiralOrderFixed(matrix [][]int) []int {
    if len(matrix) == 0 {
        return []int{}
    }

    row := len(matrix)
    col := len(matrix[0])

    res := make([]int, 0, row*col)
    left, right, top, bottom := 0, col-1, 0, row-1

    for left <= right && top <= bottom {
        // 向右遍历
        for i := left; i <= right; i++ {
            res = append(res, matrix[top][i])
        }
        top++

        // 向下遍历（需要先检查边界）
        if top <= bottom {
            for i := top; i <= bottom; i++ {
                res = append(res, matrix[i][right])
            }
            right--
        }

        // 向左遍历（需要先检查边界）
        if left <= right && top <= bottom {
            for i := right; i >= left; i-- {
                res = append(res, matrix[bottom][i])
            }
            bottom--
        }

        // 向上遍历（需要先检查边界）
        if left <= right && top <= bottom {
            for i := bottom; i >= top; i-- {
                res = append(res, matrix[i][left])
            }
            left++
        }
    }

    return res
}

错误的根本原因：

这个错误的根本原因是没有考虑边界条件。在处理矩阵类问题时，尤其需要注意：

  1. 边界交叉检查：确保索引边界（如 left <= right 和 top <= bottom）始终有效
  2. 特殊情况处理：矩阵可能是单行、单列、甚至空矩阵
  3. 方向转换条件：每次改变遍历方向前需要验证还有元素需要遍历

这是矩阵遍历问题中最容易被忽视的细节，也是导致代码出错的常见原因。

正确实现

方法一：按层模拟（推荐）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
func spiralOrder(matrix [][]int) []int {
    row := len(matrix)
    col := len(matrix[0])

    res := make([]int, row*col)
    cnt := 0

    // 初始化四个边界
    left, right, top, bottom := 0, col-1, 0, row-1

    for left <= right && top <= bottom {
        // 1. 从左到右遍历上边界
        for i := left; i <= right; i++ {
            res[cnt] = matrix[top][i]
            cnt++
        }
        top++ // 上边界下移一行

        // 2. 从上到下遍历右边界
        for i := top; i <= bottom; i++ {
            res[cnt] = matrix[i][right]
            cnt++
        }
        right-- // 右边界左移一列

        // 3. 从右到左遍历下边界（需要检查是否还有行要遍历）
        if top <= bottom {
            for i := right; i >= left; i-- {
                res[cnt] = matrix[bottom][i]
                cnt++
            }
            bottom-- // 下边界上移一行
        }

        // 4. 从下到上遍历左边界（需要检查是否还有列要遍历）
        if left <= right {
            for i := bottom; i >= top; i-- {
                res[cnt] = matrix[i][left]
                cnt++
            }
            left++ // 左边界右移一列
        }
    }

    return res
}

执行过程分析：

对于示例矩阵 [[1,2,3],[4,5,6],[7,8,9]]：

第一轮循环：

  • 初始边界：left=0, right=2, top=0, bottom=2
  • 从左到右：添加 [1,2,3]，top 变为 1
  • 从上到下：添加 [6,9]，right 变为 1
  • 从右到左：添加 [8,7]，bottom 变为 1
  • 从下到上：添加 [4]，left 变为 1

第二轮循环：

  • 边界：left=1, right=1, top=1, bottom=1
  • 从左到右：添加 [5]
  • 结束循环，因为所有元素都已访问

最终结果：[1,2,3,6,9,8,7,4,5]

方法二：改进的方向数组方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
func spiralOrder(matrix [][]int) []int {
    rows, cols := len(matrix), len(matrix[0])
    total := rows * cols

    // 创建结果数组
    result := make([]int, total)

    // 创建访问标记数组
    visited := make([][]bool, rows)
    for i := range visited {
        visited[i] = make([]bool, cols)
    }

    // 定义四个方向：右、下、左、上
    directions := [][]int{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}
    dirIndex := 0

    row, col := 0, 0
    for i := 0; i < total; i++ {
        // 添加当前元素到结果
        result[i] = matrix[row][col]
        // 标记当前位置为已访问
        visited[row][col] = true

        // 计算下一个位置
        nextRow, nextCol := row + directions[dirIndex][0], col + directions[dirIndex][1]

        // 检查是否需要改变方向
        if nextRow < 0 || nextRow >= rows || nextCol < 0 || nextCol >= cols || visited[nextRow][nextCol] {
            // 改变方向（顺时针）
            dirIndex = (dirIndex + 1) % 4
            nextRow, nextCol = row + directions[dirIndex][0], col + directions[dirIndex][1]
        }

        row, col = nextRow, nextCol
    }

    return result
}

执行过程分析：

对于同样的示例，方法二的执行过程：

  1. 从 (0,0) 开始，标记为已访问，添加值 1
  2. 当前方向为右，下一步是 (0,1)，有效且未访问，移动并添加值 2
  3. 继续向右到 (0,2)，添加值 3
  4. 尝试继续向右到 (0,3)，超出边界，方向改为向下，移动到 (1,2)，添加值 6
  5. 继续向下到 (2,2)，添加值 9
  6. 尝试继续向下，超出边界，方向改为向左，移动到 (2,1)，添加值 8
  7. 继续向左到 (2,0)，添加值 7
  8. 尝试继续向左，超出边界，方向改为向上，移动到 (1,0)，添加值 4
  9. 尝试继续向上到 (0,0)，已经访问过，方向改为向右，移动到 (1,1)，添加值 5
  10. 所有单元格都已访问，结束循环

最终结果：[1,2,3,6,9,8,7,4,5]

方法比较

方面 按层模拟（边界法） 方向数组法
思路 将矩阵分为多层，由外向内遍历 使用方向数组控制移动，遇到边界或已访问位置时转向
空间复杂度 O(1)（不计算结果数组） O(m×n)（需要访问标记数组）
易理解性 更直观，易于可视化 需要理解方向变化逻辑
实现复杂度 需要处理边界条件和单行/单列情况 需要维护访问标记
推荐度 ★★★★★ ★★★☆☆

复杂度分析

对于两种方法：

  • 时间复杂度：O(m×n)，其中 m 和 n 分别是矩阵的行数和列数。矩阵中的每个元素都被访问一次。
  • 空间复杂度：
    • 按层模拟：O(1)，只需要常数级别的额外空间（不计算结果数组）。
    • 方向数组方法：O(m×n)，需要一个与矩阵大小相同的访问标记数组。

总结

螺旋矩阵问题是一个经典的矩阵遍历问题，有两种主要解法：

  1. 按层模拟（边界法）：通过控制四个边界（左、右、上、下）来模拟螺旋遍历过程，空间效率高，思路直观。
  2. 方向数组法：使用方向数组和已访问标记来控制遍历方向，需要额外空间但思路也较为清晰。

在实际应用中，按层模拟的方法通常是更好的选择，因为它不需要额外的访问标记数组，空间复杂度更低，并且逻辑也相对直观。

这道题目的核心在于理解如何控制边界和方向，以及如何处理遍历过程中的边界情况。解决此类问题的关键是清晰地定义状态变量并正确地更新它们。