LeetCode 160 - 相交链表（Intersection of Two Linked Lists）

Problem Description

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

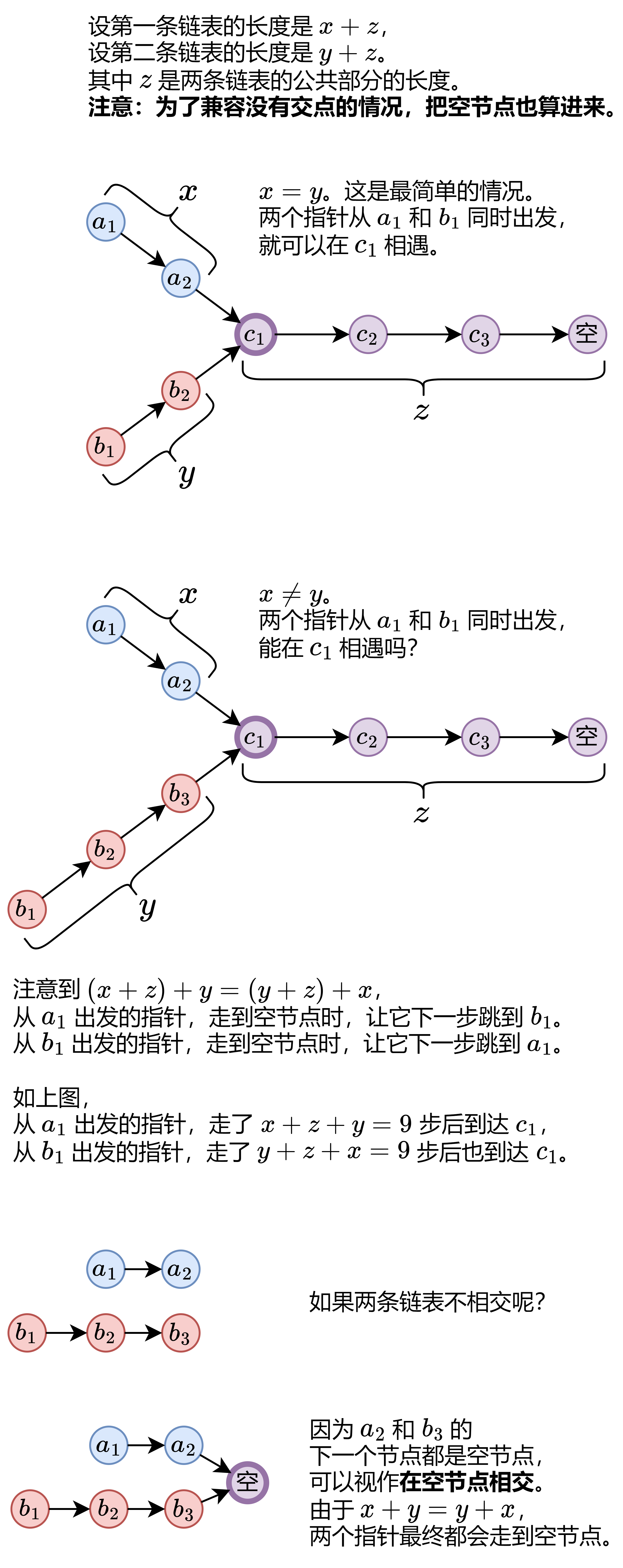
图示两个链表在节点 c1 开始相交：

A:      a1 → a2
                ↘
                  c1 → c2 → c3
                ↗          
B: b1 → b2 → b3

题目数据保证整个链式结构中不存在环，函数返回结果后，链表必须保持其原始结构。

示例 1：

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at ‘8’
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

示例 2：

输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at ‘2’

示例 3：

1
2
3

2 → 6 → 4

1 → 5

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：No intersection

约束条件：

listA 中节点数目为 m
listB 中节点数目为 n
1 <= m, n <= 3 * 10^4
1 <= Node.val <= 10^5
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点，intersectVal 为 0
如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

进阶：你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案？

Solution Approach

这个问题有几种解法，我们将逐一介绍，并分析各自的优缺点。

方法一：哈希表法

核心思想：使用哈希表存储第一个链表的所有节点，然后遍历第二个链表，检查每个节点是否在哈希表中存在。

实现步骤：

创建一个哈希表（Go中可以使用map）
将链表A的所有节点添加到哈希表中
遍历链表B，对于每个节点，检查它是否已经存在于哈希表中
如果找到匹配的节点，则返回该节点作为交点
如果遍历完链表B仍未找到匹配节点，则返回nil

func getIntersectionNode(headA, headB *ListNode) *ListNode {
    nodeMap := make(map[*ListNode]bool)
  
    // 将链表A的所有节点添加到哈希表
    for curr := headA; curr != nil; curr = curr.Next {
        nodeMap[curr] = true
    }
  
    // 遍历链表B，检查节点是否在哈希表中
    for curr := headB; curr != nil; curr = curr.Next {
        if nodeMap[curr] {
            return curr
        }
    }
  
    return nil
}

方法二：双指针法（最优解）

核心思想：使用两个指针 pA 和 pB 分别遍历链表 A 和链表 B。当一个指针到达链表末尾时，将其重定向到另一个链表的头部。最终，两个指针会在相交点相遇，或者在遍历完两个链表后同时为 nil。

重定向过程的深入解释

为什么需要重定向？

这个问题的核心挑战在于两个链表可能长度不同。如果不进行重定向，两个指针永远不会在正确的位置相遇。

直观理解：

想象两个人在两条不同的道路上跑步，这两条道路在某一点相交。如果两个人以相同的速度跑步，但起点不同，他们可能永远不会在相交点相遇。重定向就像是让一个人跑完自己的路后，立即从另一个人的起点开始跑，这样他们最终会在相交点相遇。

数学证明：

设链表A的长度为m，链表B的长度为n，从交点到末尾的公共部分长度为k。

链表A中交点到末尾的距离：m-k
链表B中交点到末尾的距离：n-k

重定向后，两个指针走过的总路径：

pA: m + (n-k) = m + n - k
pB: n + (m-k) = n + m - k

所以两个指针走过的总距离是相等的！这就是为什么它们会在交点相遇。

具体例子演示：

1 2	A: a1 → a2 → c1 → c2 → c3 B: b1 → b2 → b3 → c1 → c2 → c3

其中c1是交点。

步骤详解：

初始状态：
- pA = a1, pB = b1
第一次遍历：
- pA: a1 → a2 → c1 → c2 → c3 → nil
- pB: b1 → b2 → b3 → c1 → c2 → c3 → nil
重定向过程：
- pA到达nil，重定向到b1
- pB到达nil，重定向到a1
第二次遍历：
- pA: b1 → b2 → b3 → c1
- pB: a1 → a2 → c1
相遇：两个指针在c1相遇！

为什么重定向有效？

长度相同的情况：重定向确保两个指针在相同的相对位置开始比较
长度不同的情况：重定向让较短的链表的指针"等待"较长的链表的指针，直到它们在相同的相对位置
没有交点的情况：重定向确保两个指针都会遍历完两个链表，最终同时变为nil

重定向的巧妙之处：

无需预计算长度：不需要先遍历链表计算长度
空间复杂度O(1)：只需要两个指针
时间复杂度O(m+n)：每个指针最多遍历两个链表各一次
自动处理边界情况：自然地处理了空链表、单节点等特殊情况

实现步骤：

初始化两个指针 pA 和 pB 分别指向链表 A 和链表 B 的头节点
同时移动这两个指针，每次移动一步
当 pA 到达链表 A 的末尾时，将其重定向到链表 B 的头部
当 pB 到达链表 B 的末尾时，将其重定向到链表 A 的头部
如果两个链表相交，pA 和 pB 最终会在相交点相遇
如果两个链表不相交，pA 和 pB 最终都会变为 nil

func getIntersectionNode(headA, headB *ListNode) *ListNode {
    if headA == nil || headB == nil {
        return nil
    }
  
    pA, pB := headA, headB
  
    for pA != pB {
        // 当到达链表末尾时，切换到另一个链表的头部
        if pA == nil {
            pA = headB
        } else {
            pA = pA.Next
        }
      
        if pB == nil {
            pB = headA
        } else {
            pB = pB.Next
        }
    }
  
    return pA // pA 要么是相交点，要么是 nil
}

方法三：计算长度差法

核心思想：计算两个链表的长度，然后让较长的链表先移动差值步数，之后两个指针同步前进，最终会在相交点相遇。

实现步骤：

分别计算链表 A 和链表 B 的长度
计算两个链表的长度差 diff
让较长的链表的指针先移动 diff 步
然后两个指针同步前进，每次都移动一步
检查两个指针是否相等，如果相等，则返回该节点

func getIntersectionNode(headA, headB *ListNode) *ListNode {
    // 计算链表长度的辅助函数
    getLength := func(head *ListNode) int {
        length := 0
        for curr := head; curr != nil; curr = curr.Next {
            length++
        }
        return length
    }
  
    lenA, lenB := getLength(headA), getLength(headB)
    pA, pB := headA, headB
  
    // 让较长的链表先移动差值步数
    if lenA > lenB {
        for i := 0; i < lenA - lenB; i++ {
            pA = pA.Next
        }
    } else {
        for i := 0; i < lenB - lenA; i++ {
            pB = pB.Next
        }
    }
  
    // 同步前进，寻找相交点
    for pA != pB {
        pA = pA.Next
        pB = pB.Next
    }
  
    return pA // pA 要么是相交点，要么是 nil
}

错误解法分析

我之前的解法存在以下问题：

func getIntersectionNode(headA, headB *ListNode) *ListNode {
    if headA == nil || headB == nil {
        return nil
    }

    fast, slow := headA, headB
    for fast != slow {
        if fast == nil {
            fast = headB
        } else {
            fast = fast.Next
        }
        if fast == nil {
            fast = headB
        } else {
            fast = fast.Next
        }

        if slow == nil {
            slow = headA
        } else {
            slow = slow.Next
        }
    }
    return fast
}

错误点：

算法思路混淆：这个解法似乎混合了检测环形链表的快慢指针法和检测相交链表的双指针法。在相交链表问题中，不应该使用不同速度的指针。
指针移动逻辑错误：fast 指针尝试每次移动两步，而 slow 指针每次移动一步。这种方式在没有环的情况下可能导致无法正确找到相交点。
重置逻辑问题：代码中 fast 指针可能在同一次循环中被重置两次，这不符合算法的要求。
可能的无限循环：如果两个链表不相交，并且长度不同，这种实现可能导致指针永远不会相等，从而陷入无限循环。

解法比较

方面	哈希表法	双指针法	长度差法
时间复杂度	O(m+n)	O(m+n)	O(m+n)
空间复杂度	O(m)	O(1)	O(1)
优点	简单直观，容易实现	空间复杂度最优，代码简洁	思路清晰，易于理解
缺点	需要额外空间	初次理解可能有难度	代码略长，需要计算长度
推荐度	★★★☆☆	★★★★★	★★★★☆

Key Learnings

双指针技巧：此问题展示了双指针在解决链表问题中的强大作用，特别是方法二的解法巧妙且优雅。
空间时间权衡：哈希表法虽然直观，但需要额外空间；而双指针法和长度差法只需O(1)空间，展示了算法设计中空间与时间的权衡。
边界条件处理：在处理链表问题时，总是需要考虑空链表、单节点链表等边界情况。
问题简化：通过重定向指针（方法二）或提前移动（方法三），我们能够简化问题，使不同长度的链表在同步点相遇。
错误分析：理解错误解法的缺陷能够帮助我们更深入地理解问题的本质和解决方案的要求。在此问题中，不恰当地混用算法模式（快慢指针和双指针）导致了解法的失败。