LeetCode 114 - 二叉树展开为链表

修订记录

版本	修订时间	修订内容
v1.0	2025-04-29 20:08:43	初始版本，包含错误解法分析和修正解法
v2.0	2025-06-15 13:11:33	添加进一步优化版本，完善解法对比和学习总结

问题描述

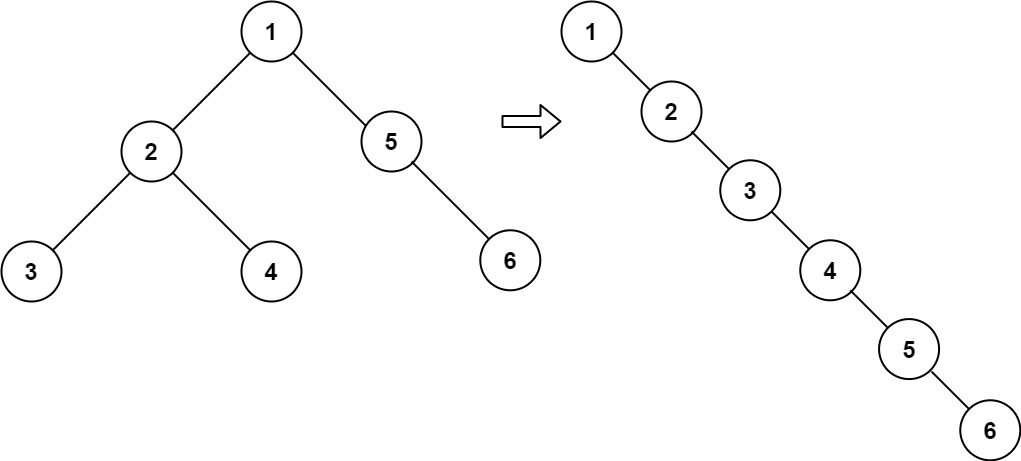
给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树先序遍历顺序相同。

示例 1：

1 2	输入：root = [1,2,5,3,4,null,6] 输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

1 2	输入：root = [] 输出：[]

示例 3：

1 2	输入：root = [0] 输出：[0]

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

错误解法与分析

我的初始解法是：

// 传入参数为一颗子树的根节点，返回值为处理完后这颗子树的最后一个节点
func dfsFlatten(node *TreeNode) *TreeNode {
    if node == nil {
        return nil
    }
    
    leftEnd := dfsFlatten(node.Left)
    rightEnd := dfsFlatten(node.Right)
    
    if leftEnd != nil {
        leftEnd.Right = node.Right
        node.Right = node.Left
    }
    
    if rightEnd == nil {
        return node  // ❌ 错误点：当右子树为空时，应该返回leftEnd而不是node
    }
    
    return rightEnd
}

这个解法在某些测试用例中失败了，主要有以下几个错误：

错误原因分析

没有设置 node.Left = nil
题目明确要求展开后的单链表左子指针始终为 null。在我的错误代码中，当处理完左子树后（leftEnd := dfsFlatten(node.Left)），并且 leftEnd != nil 时，我执行了 node.Right = node.Left，将原来的左子树挂载到了右子树的位置。但是，我忘记了将 node.Left 设置为 nil。这导致原本的左子树引用依然存在，不满足题目要求的链表结构。正确的做法是在 node.Right = node.Left 之后，紧接着执行 node.Left = nil，彻底断开左子树的连接。
缺少对叶子节点的特殊处理（优化缺失）
虽然这不算一个导致结果错误的 bug，但它是一个重要的优化点。叶子节点（node.Left == nil && node.Right == nil）是递归的最小单元，它们自身就是展开后的链表的末尾节点。在错误代码中，即使遇到叶子节点，仍然会继续递归调用 dfsFlatten(nil) 两次，然后才返回。正确的解法中增加了 if node.Left == nil && node.Right == nil { return node } 的判断，可以直接返回叶子节点本身，避免了不必要的递归调用，提高了效率。
返回值逻辑错误 (rightEnd == nil 的情况)
这是最关键的逻辑错误。dfsFlatten 函数的定义是：传入一个子树的根节点 node，将其原地展开为链表，并返回这个展开后链表的最后一个节点。
- 当 rightEnd == nil 时，意味着当前节点 node 没有右子树（或者右子树递归展开后返回 nil）。
- 在这种情况下，如果 leftEnd != nil（即存在左子树且已展开），那么根据先序遍历的顺序，node 之后应该连接的是展开后的左子树。因此，整个以 node 为根的展开链表的最后一个节点，就应该是其左子树展开后的最后一个节点，即 leftEnd。
- 我的错误代码中返回了 node。这在只有左子树的情况下是错误的，因为 node 并不是展开后链表的最后一个节点。
- 如果 leftEnd == nil（左右子树都为空），此时 node 本身就是最后一个节点。看起来返回 node 似乎是对的。但是，这种情况其实已经被第 2 点提到的叶子节点判断覆盖了（在正确解法中）。在错误解法中，由于缺少叶子节点判断，即使左右子树都为空，也会执行到这里，并错误地返回 node，但这恰好在“叶子节点”这个特定场景下得到了“正确”的结果，掩盖了逻辑本身的缺陷。正确的逻辑应该是，当 rightEnd == nil 时，无论 leftEnd 是否为 nil，都应该返回 leftEnd（因为如果 leftEnd 为 nil，返回 nil 也是符合逻辑的，虽然会被叶子节点优化覆盖）。

示例追踪

让我们用一个具体的例子 [1, 2, null, 3, 4] 来追踪错误代码的执行：

期望输出: 1 -> 2 -> 3 -> 4 (所有左指针为 nil)

错误代码追踪:

dfsFlatten(1)
- dfsFlatten(2)
  - dfsFlatten(3): (叶子) -> 错误返回 node 3
  - dfsFlatten(4): (叶子) -> 错误返回 node 4
  - 处理 node 2:
    - leftEnd = 3, rightEnd = 4
    - 3.Right = 2.Right (node 2 原右子节点 4) => 3.Right = 4
    - 2.Right = 2.Left (node 2 原左子节点 3) => 2.Right = 3
    - 遗漏 2.Left = nil
    - 返回 rightEnd (node 4)
- leftEnd = 4 (来自 dfsFlatten(2))
- dfsFlatten(nil) (node 1 的右子节点) -> 返回 nil
- rightEnd = nil
- 处理 node 1:
  - leftEnd = 4, rightEnd = nil
  - 4.Right = 1.Right (nil) => 4.Right = nil
  - 1.Right = 1.Left (node 2) => 1.Right = 2
  - 遗漏 1.Left = nil
  - rightEnd == nil -> 错误返回 node (node 1)

最终结果: 函数返回 node 1，但链表结构是错误的：1 的 Left 仍然指向 2，2 的 Left 仍然指向 3。此外，由于返回值错误，如果上层还有调用，也会基于错误的末尾节点信息继续拼接，导致链表结构混乱。

正确解法

经过分析，我改进的解法是：

func dfsFlatten(node *TreeNode) *TreeNode {
    if node == nil {
        return nil
    }
    
    if node.Left == nil && node.Right == nil {
        return node
    }
    
    leftEnd := dfsFlatten(node.Left)
    rightEnd := dfsFlatten(node.Right)
    
    if leftEnd != nil {
        leftEnd.Right = node.Right
        node.Right = node.Left
        node.Left = nil  // 确保左指针设为null
    }
    
    if rightEnd == nil {
        return leftEnd  // 如果右子树为空，返回leftEnd
    }
    
    return rightEnd
}

为什么这个解法可以工作

正确处理左子指针：将 node.Left = nil 确保了展开后的链表左子指针始终为null。
叶子节点优化：添加了对叶子节点的判断，可以提前返回，减少不必要的处理。
返回值逻辑正确：
- 当右子树存在时，返回右子树展开后的末尾节点
- 当右子树为空时，返回左子树展开后的末尾节点
- 当左右子树都为空时，返回节点本身

进一步优化版本 [v2.0 新增]

在深入理解问题后，我们可以写出一个更清晰的优化版本：

func flatten(root *TreeNode) {
    var dfs func(root *TreeNode) *TreeNode
    dfs = func(root *TreeNode) *TreeNode {
        // 空节点或叶子节点直接返回
        if root == nil || (root.Left == nil && root.Right == nil) {
            return root
        }
        
        // 保存原始右子树
        tmpRight := root.Right
        
        // 先处理左子树
        leftLast := dfs(root.Left)
        
        // 如果左子树存在，进行连接操作
        if leftLast != nil {
            leftLast.Right = root.Right    // 左子树的末尾连接到原右子树
            root.Right = root.Left         // 左子树移到右边
            root.Left = nil                // 清空左子树
        }
        
        // 如果原来没有右子树，返回左子树的末尾
        if tmpRight == nil {
            return leftLast
        }
        
        // 处理原右子树，返回其末尾节点
        return dfs(tmpRight)
    }
    
    dfs(root)
}

优化版本的核心思想

分离处理：先处理左子树，完成左子树的连接操作，再处理右子树
保存引用：使用 tmpRight 保存原始右子树，避免在连接过程中丢失引用
清晰的逻辑流程：
- 处理左子树得到 leftLast
- 如果左子树存在，执行连接操作
- 根据是否有原右子树决定返回值

与之前解法的对比

方面	初始错误解法	修正解法	优化版本
左右子树处理	同时处理	同时处理	分离处理
右子树引用	直接使用	直接使用	提前保存
代码可读性	较差	良好	更好
逻辑清晰度	混乱	清晰	非常清晰

执行过程示例

以树 [1,2,5,3,4,null,6] 为例：

优化版本执行流程：

dfs(1):
- tmpRight = 5
- leftLast = dfs(2) 返回节点4
- 连接：4.Right = 5, 1.Right = 2, 1.Left = nil
- tmpRight != nil，返回 dfs(5) 的结果
dfs(2):
- tmpRight = null
- leftLast = dfs(3) 返回节点3
- 连接：3.Right = null, 2.Right = 3, 2.Left = nil
- tmpRight == nil，返回 leftLast (节点3)
- 但还要处理右子树4，最终返回节点4

这个优化版本的逻辑更加直观，代码也更容易理解和维护。

学习总结

细节很重要：在树和链表相关问题中，指针操作的细节非常重要，漏掉一步可能导致整个结构错误。
返回值的含义要明确：在递归函数中，返回值的含义必须清晰且一致。我最初混淆了返回值的含义，导致了逻辑错误。
多思考边界情况：叶子节点、空节点等边界情况需要特别注意。
前序思考：在编写递归函数前，应该先明确函数参数和返回值的具体含义，并确保整个递归过程中这个含义保持一致。
分离复杂逻辑：当处理逻辑较复杂时，可以考虑分离处理，如优化版本中先处理左子树再处理右子树的方式。
保护重要引用：在进行指针操作时，要注意保护可能被修改的重要引用，避免在操作过程中丢失。