❌ LeetCode 98 - 验证二叉搜索树 (Validate Binary Search Tree)

问题描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

1 2	输入：root = [2,1,3] 输出：true

示例 2：

1
2
3

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在 [1, 10^4] 内
-2^31 <= Node.val <= 2^31 - 1

错误解法与分析

我的初始解法是使用递归方法，为每个节点设定上下界来验证二叉搜索树的性质：

func isValidBST(root *TreeNode) bool {
    return helplerIsValidBST(root, math.MinInt64, math.MaxInt64)
}

func helplerIsValidBST(node *TreeNode, low, high int) bool {
    if node == nil {
        return true
    }
  
    // ❌ 错误点：使用了错误的比较运算符
    if node.Val < low || node.Val > high {
        return false
    }
  
    return helplerIsValidBST(node.Left, low, node.Val) && 
           helplerIsValidBST(node.Right, node.Val, high)
}

这个解法在以下测试用例中失败了：

1
2
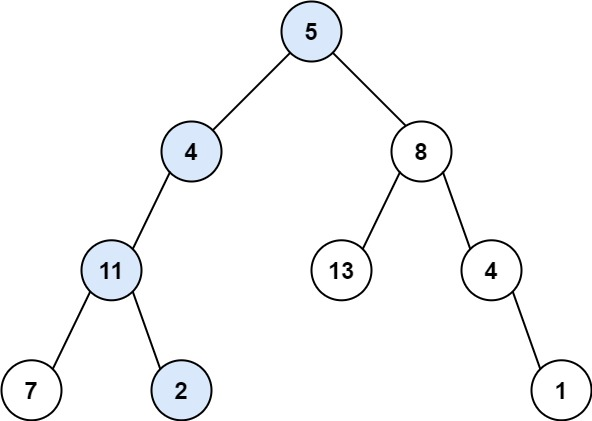
3

输入：[5,4,6,null,null,3,7]
预期输出：false
实际输出：true

错误原因分析

这个测试用例表示一棵二叉树，其中根节点是 5，左子节点是 4，右子节点是 6，而 6 的左子节点是 3，右子节点是 7。

我的错误在于条件判断：

1
2
3

if node.Val < low || node.Val > high {
    return false
}

这个判断条件有两个问题：

错误的不等号方向：根据二叉搜索树的定义，左子树的所有节点应该小于当前节点，右子树的所有节点应该大于当前节点。而我使用的条件是检查节点值是否在范围 [low, high] 之内，这与题目要求不符。
没有处理相等的情况：二叉搜索树不允许出现相等的值。例如，当检查右子树时，所有节点值必须严格大于父节点，而我的判断条件并没有排除等于父节点值的情况。

在测试用例 [5,4,6,null,null,3,7] 中，节点 6 的左子节点是 3，这违反了二叉搜索树的性质（6的左子树所有节点都应该大于5且小于6），但我的解法没有正确识别这个错误。

正确解法

经过分析，我改进的解法是：

func isValidBST(root *TreeNode) bool {
    return helplerIsValidBST(root, math.MinInt64, math.MaxInt64)
}

func helplerIsValidBST(node *TreeNode, low, high int) bool {
    if node == nil {
        return true
    }
  
    // ✓ 修复：使用正确的比较运算符，确保严格大于小于关系
    if node.Val <= low || node.Val >= high {
        return false
    }
  
    return helplerIsValidBST(node.Left, low, node.Val) && 
           helplerIsValidBST(node.Right, node.Val, high)
}

为什么这个解法可以工作

修正后的代码使用了正确的比较运算符：

1
2
3

if node.Val <= low || node.Val >= high {
    return false
}

这个条件判断的含义是：

node.Val <= low 检查当前节点值是否小于等于下界，如果是，违反了BST性质
node.Val >= high 检查当前节点值是否大于等于上界，如果是，同样违反了BST性质

这样，我们确保了：

左子树的所有节点值必须严格小于当前节点值（通过设置上界为当前节点值）
右子树的所有节点值必须严格大于当前节点值（通过设置下界为当前节点值）
整个树的每个节点值都必须严格遵循它的有效范围

对于测试用例 [5,4,6,null,null,3,7]：

根节点 5 的有效范围是 (-∞, +∞)
节点 4 的有效范围是 (-∞, 5)
节点 6 的有效范围是 (5, +∞)
节点 3 的有效范围是 (5, 6)，但 3 < 5，所以不在有效范围内，返回 false

学习总结

通过这个错误，我学到了几个重要的教训：

理解问题定义的重要性：二叉搜索树定义中的"大于"和"小于"是严格的不等关系，不包含等于的情况。
边界条件处理：在处理比较关系时，要特别注意是使用严格不等式（< 和 >）还是非严格不等式（<= 和 >=）。
递归边界的设置：在递归检查二叉搜索树时，通过合适的上下界设置是确保正确性的关键。
测试用例分析：特殊结构的测试用例（如包含特定路径上的值）可以帮助发现算法中的缺陷。

这个错误提醒我在实现算法时要仔细审题，特别是对于有特定定义的数据结构，要确保实现符合其精确定义。