LeetCode 207 - 课程表（Course Schedule）

问题描述

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi]，表示如果要学习课程 ai 则必须先学习课程 bi。

例如，先修课程对 [0, 1] 表示：想要学习课程 0，你需要先完成课程 1。

请你判断是否可能完成所有课程的学习？如果可以，返回 true；否则，返回 false。

示例 1：

1
2
3

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。这是可能的。

示例 2：

1
2
3

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0；并且学习课程 0 之前，你还应先完成课程 1。这是不可能的。

约束条件：

1 <= numCourses <= 2000
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
prerequisites[i] 中的所有课程对互不相同

解题思路

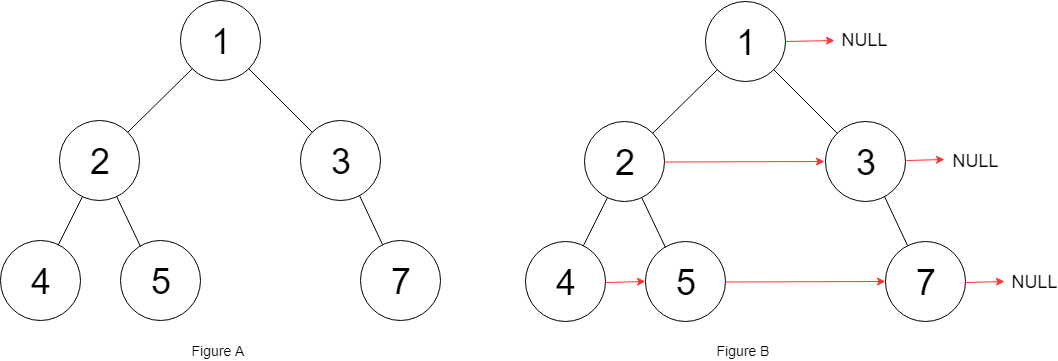
这个问题本质上是判断一个有向图是否存在环。我们可以将课程看作图中的节点，先修关系看作有向边。如果图中存在环，那么就无法完成所有课程（因为环意味着出现了循环依赖）。

对于这类问题，通常有两种解决方法：拓扑排序（BFS） 和 深度优先搜索（DFS）。

方法一：BFS 拓扑排序

拓扑排序的基本思想是：

计算图中每个节点的入度（有多少条边指向该节点）
将所有入度为 0 的节点（没有先修课程的课程）加入队列
逐个出队，将出队节点的所有相邻节点的入度减 1
如果相邻节点的入度变为 0，则将其加入队列
重复步骤 3-4，直到队列为空
如果最终访问的节点数等于总节点数，则说明不存在环，可以完成所有课程

方法二：DFS 检测环

DFS 检测环的基本思想是：

对图中的每个未访问过的节点进行 DFS
在 DFS 过程中，使用三种状态标记节点：
- 未访问（0）
- 访问中（1）：当前 DFS 路径上的节点
- 已完成（2）：节点及其所有后代都已被访问
如果 DFS 过程中遇到一个「访问中」的节点，则说明存在环
如果所有节点都能被标记为「已完成」，则说明不存在环

实现细节

BFS 拓扑排序实现

BFS 实现需要维护以下数据结构：

邻接表（adjacency list）：表示图结构
入度数组：记录每个节点的入度
队列：存储入度为 0 的节点

具体步骤：

构建邻接表和入度数组
将所有入度为 0 的节点加入队列
BFS 处理队列中的节点：
- 出队一个节点，将学习的课程数加 1
- 将其所有相邻节点的入度减 1
- 如果相邻节点的入度变为 0，则加入队列
检查学习的课程数是否等于总课程数

DFS 检测环实现

DFS 实现需要以下数据结构：

邻接表：表示图结构
访问状态数组：记录每个节点的访问状态

具体步骤：

构建邻接表
对每个未访问的节点进行 DFS：
- 如果节点在当前路径上被访问过（状态为 1），则存在环
- 如果节点已经被完全处理（状态为 2），则跳过
- 否则，标记节点为「访问中」（状态为 1）
- 递归访问所有相邻节点
- 标记节点为「已完成」（状态为 2）

代码实现

方法一：BFS 拓扑排序

func canFinish(numCourses int, prerequisites [][]int) bool {
    // 构建邻接表和入度数组
    graph := make([][]int, numCourses)    // 邻接表：graph[i] 表示学完课程i后可以学习的课程列表
    inDegree := make([]int, numCourses)   // 入度数组：inDegree[i] 表示学习课程i前需要完成的课程数量
    
    // 填充邻接表和计算入度
    for _, prereq := range prerequisites {
        course, prerequisite := prereq[0], prereq[1]
        // 添加有向边：prerequisite -> course
        graph[prerequisite] = append(graph[prerequisite], course)
        // 课程course的入度加1
        inDegree[course]++
    }
    
    // 将所有入度为0的课程加入队列（没有先修课程的课程）
    queue := []int{}
    for i := 0; i < numCourses; i++ {
        if inDegree[i] == 0 {
            queue = append(queue, i)
        }
    }
    
    // 记录已学习的课程数量
    count := 0
    
    // BFS拓扑排序
    for len(queue) > 0 {
        // 出队一个课程
        course := queue[0]
        queue = queue[1:]
        count++ // 学习这门课程
        
        // 将其指向的课程的入度减1
        for _, nextCourse := range graph[course] {
            inDegree[nextCourse]--
            // 如果入度变为0，加入队列
            if inDegree[nextCourse] == 0 {
                queue = append(queue, nextCourse)
            }
        }
    }
    
    // 如果学完的课程数等于总课程数，则可以完成所有课程
    return count == numCourses
}

方法二：DFS 检测环

func canFinish(numCourses int, prerequisites [][]int) bool {
    // 构建邻接表
    graph := make([][]int, numCourses)
    for _, prereq := range prerequisites {
        course, prerequisite := prereq[0], prereq[1]
        graph[prerequisite] = append(graph[prerequisite], course)
    }
    
    // 访问状态数组：0=未访问，1=访问中（当前路径上），2=已完成
    visited := make([]int, numCourses)
    
    // 对每个节点进行DFS，检测环
    for i := 0; i < numCourses; i++ {
        if visited[i] == 0 { // 如果未访问
            if hasCycle(graph, visited, i) {
                return false // 存在环，无法完成所有课程
            }
        }
    }
    return true // 不存在环，可以完成所有课程
}

// DFS检测环
func hasCycle(graph [][]int, visited []int, course int) bool {
    // 如果节点在当前路径上被访问过，说明有环
    if visited[course] == 1 {
        return true
    }
    // 如果节点已经被完全处理，无需再次检查
    if visited[course] == 2 {
        return false
    }
    
    // 标记为访问中
    visited[course] = 1
    
    // 递归检查所有相邻节点
    for _, nextCourse := range graph[course] {
        if hasCycle(graph, visited, nextCourse) {
            return true // 如果找到环，立即返回
        }
    }
    
    // 标记为已完成
    visited[course] = 2
    return false // 该路径上不存在环
}

方法比较

方面	BFS拓扑排序	DFS检测环
时间复杂度	O(V+E)	O(V+E)
空间复杂度	O(V+E)	O(V+E)
实现难度	中等	中等
优点	直观理解入度和依赖关系，容易得到拓扑序列	递归实现简洁，可以更快检测到环
缺点	需要额外维护入度数组	递归调用可能导致栈溢出（但在此题约束下不会）
适用场景	需要拓扑序列，或初学者理解图算法	只需判断是否存在环，或递归思维更适合
推荐度	★★★★☆	★★★★★

复杂度分析

两种方法的时间和空间复杂度都是：

时间复杂度：O(V+E)，其中 V 是节点数（课程数），E 是边数（先修关系数）
空间复杂度：O(V+E)，用于存储图结构和辅助数组

具体分析：

BFS：需要邻接表 O(V+E)、入度数组 O(V) 和队列 O(V)
DFS：需要邻接表 O(V+E)、访问状态数组 O(V) 和递归调用栈 O(V)

关键收获

图的表示方法：使用邻接表表示图结构，适合稀疏图
拓扑排序应用：拓扑排序可以解决依赖关系问题，如课程安排、任务调度等
状态标记技巧：在DFS中使用三种状态（未访问、访问中、已完成）可以有效检测环
队列的应用：在BFS中使用队列管理入度为0的节点

常见陷阱：

混淆了有向边的方向：注意 [ai, bi] 表示 bi → ai，即学习 ai 前必须完成 bi
忘记检查最终访问的节点数：在BFS中，即使队列为空，也要检查是否访问了所有节点
DFS检测环时忘记标记节点状态：必须正确标记节点为"访问中"和"已完成"

相关问题：

LeetCode 210：课程表 II（Course Schedule II）- 在本题基础上输出拓扑排序序列
LeetCode 802：找到最终的安全状态（Find Eventual Safe States）- 找出不在任何环中的节点