Adrian Wang's blog

一个完全由AI生成，但是内容高质量的Blog

Redis 数据结构：跳表详解

Posted on Edited on In , , ,
Symbols count in article: 5.8k Reading time ≈ 5 mins.
深度解析 Redis 跳表（skiplist）的原理、实现细节和性能特性，探讨其在有序集合（Sorted Set）中的应用以及相比于其他数据结构的优势。

跳表

什么是跳表？

跳表（Skip List）可以简单理解为"带电梯的多层楼房"。想象一下：

  • 普通链表就像一层楼的走廊，要找某个房间只能一个一个房间地走过去
  • 跳表就像多层楼房，上层楼有"快速通道"，可以快速跳跃到目标区域，然后再到下层精确查找

Redis 只有 Zset（有序集合）对象的底层实现用到了跳表，跳表的优势是能支持平均 O(logN) 复杂度的节点查找。

为什么 Zset 同时使用跳表和哈希表？

zset 结构体里有两个数据结构：一个是跳表，一个是哈希表。这样设计的好处是：

  • 跳表负责范围查询：比如查找分数在 80-90 之间的所有学生
  • 哈希表负责单点查询：比如快速查找张三的具体分数
1
2
3
4
typedef struct zset {
    dict *dict;
    zskiplist *zsl;
} zset;

数据一致性是如何保证的？

Zset 对象在执行数据插入或更新时，会同时在跳表和哈希表中进行相同操作，确保两个数据结构的信息保持一致。就像酒店的房间登记系统，既要在楼层分布图上标记，也要在客户信息表中记录。

具体来说：

  • 支持范围查询（如 ZRANGEBYSCORE 操作）：依靠跳表的有序特性
  • 支持快速单点查询（如 ZSCORE 操作）：依靠哈希表的 O(1) 查找

为什么通常只说跳表是 Zset 的底层结构？

虽然 Zset 实际使用的是「哈希表 + 跳表」的组合结构，但我们讨论时通常只提跳表，是因为：

  • 哈希表主要起辅助作用，用于快速获取元素权重
  • 核心操作都是由跳表实现的，比如范围查询、排序等
  • 跳表决定了 Zset 的主要特性和性能表现

接下来，详细的说下跳表。

跳表结构设计

在理解跳表之前，我们先看看普通链表的问题。

普通链表的查找问题：
链表在查找元素时，只能从头开始一个一个节点地遍历，就像在一条长长的队伍中找人，只能从队头开始一个个问过去，效率很低，时间复杂度是 O(N)。

跳表的解决方案：
跳表是在链表基础上改进过来的，实现了一种「多层」的有序链表。就像给队伍安排了多个"队长"，可以先问队长大概位置，再在小范围内精确查找，这样能快速定位数据。

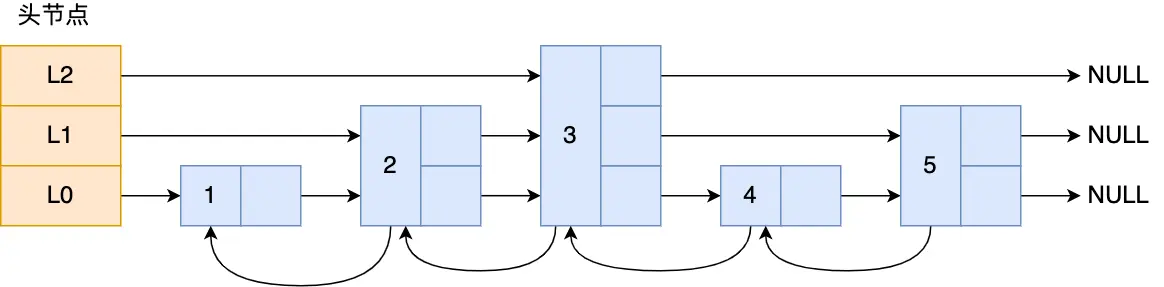
那跳表长什么样呢？我这里举个例子，下图展示了一个层级为 3 的跳表。

1748326331702

图中头节点有 L0~L2 三个头指针，分别指向了不同层级的节点，然后每个层级的节点都通过指针连接起来：

  • L0 层级（最底层）：共有 5 个节点，分别是节点 1、2、3、4、5（包含所有节点）
  • L1 层级（中间层）：共有 3 个节点，分别是节点 2、3、5（部分节点）
  • L2 层级（最高层）：只有 1 个节点，也就是节点 3（更少节点）

查找效率对比：

  • 普通链表：要找节点 4，需要从头开始：1→2→3→4，查找 4 次
  • 跳表查找：只需要 2 次跳跃：
    1. 从 L2 层直接跳到节点 3
    2. 从节点 3 在 L0 层向前一步找到节点 4

可以看到，这个查找过程就是在多个层级上跳来跳去，最后定位到元素。当数据量很大时，跳表的查找复杂度就是 O(logN)。

跳表节点是怎么实现多层级的？

要理解跳表的多层级结构，我们需要看看「跳表节点」的数据结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
typedef struct zskiplistNode {
    //Zset 对象的元素值
    sds ele;
    //元素权重值
    double score;
    //后向指针
    struct zskiplistNode *backward;
  
    //节点的 level 数组，保存每层上的前向指针和跨度
    struct zskiplistLevel {
        struct zskiplistNode *forward;
        unsigned long span;
    } level[];
} zskiplistNode;

让我们逐个分析这个结构体的字段：

1. 数据存储字段：

  • sds ele：存储 Zset 对象的元素值（比如学生姓名"张三"）
  • double score：存储元素的权重值（比如学生分数 85.5）

2. 后向指针：

  • struct zskiplistNode *backward：指向前一个节点
  • 作用：方便从跳表尾节点开始倒序遍历，就像可以从队尾往前走一样

3. 关键的多层级实现：

  • struct zskiplistLevel level[]：这是实现多层级的关键！

level 数组是如何工作的？

  • level 数组中的每个元素代表跳表的一层
  • level[0] 表示第一层（L0），level[1] 表示第二层（L1），以此类推
  • 每层包含两个信息：
    • forward：指向下一个跳表节点的指针
    • span：跨度，记录两个节点之间的距离

比如，下面这张图，展示了各个节点的跨度。

1748326342079

跨度（span）的作用是什么？

很多人第一眼看到跨度，会以为是用来辅助遍历的，但实际上并不是。遍历操作只需要用前向指针（forward）就可以完成了。

跨度的真正作用：计算节点排位

  • 跳表中的节点都是按分数排序的
  • 要计算某个节点在跳表中的排位（排第几名），就需要用到跨度
  • 计算方法：从头节点到目标节点的查找路径上，将沿途经过的所有层的跨度累加起来

举个例子：
查找图中节点 3 在跳表中的排位：

  1. 从头节点开始查找节点 3
  2. 查找过程只经过了一个层（L2）
  3. L2 层的跨度是 3
  4. 所以节点 3 在跳表中的排位是第 3 名

这就像马拉松比赛中的距离标记，通过累加经过的距离标记，可以知道跑了多远。

头节点的特殊性：
图中的头节点其实也是 zskiplistNode 跳表节点，只不过头节点比较特殊：

  • 后向指针、权重、元素值都没有用到（所以图中省略了）
  • 主要作用是作为各层链表的起始点

跳表的整体管理结构：
那么，由谁来管理整个跳表，定义哪个节点是头节点呢？这就需要介绍「跳表」结构体了：

1
2
3
4
5
typedef struct zskiplist {
    struct zskiplistNode *header, *tail;
    unsigned long length;
    int level;
} zskiplist;

跳表结构里包含了四个重要信息：

  • header/tail：跳表的头尾节点指针

    • 好处：可以在 O(1) 时间内直接访问头节点和尾节点
    • 就像电梯楼层显示器，可以直接知道最高层和最低层

  • length：跳表的节点数量

    • 好处：可以在 O(1) 时间内获取跳表有多少个节点
    • 就像楼房的住户统计表，直接知道总共有多少住户

  • level：跳表的最大层数

    • 好处：可以在 O(1) 时间内知道跳表的最高层是第几层
    • 就像建筑物的楼层标识，直接知道这栋楼有多高

跳表节点查询过程

跳表查找的基本策略：
跳表查找就像在多层停车场找车位一样，先从最高层快速定位区域，再逐层下降精确查找。

具体查找过程：
跳表会从头节点的最高层开始，逐一遍历每一层。在每一层查找时，有明确的判断规则：

何时继续在当前层前进？
满足以下任一条件就继续在当前层向前移动：

  1. 权重比较：下一个节点的权重 < 目标权重
  2. 相同权重时的元素比较：下一个节点的权重 = 目标权重，但元素值 < 目标元素值

何时跳到下一层？
如果上面两个条件都不满足，或者下一个节点为空，就跳到下一层继续查找。

这个策略确保了：

  • 在每一层都能快速跳过明显不符合的节点
  • 权重相同时还能根据元素值进行精确比较
  • 逐层下降，最终精确定位目标节点

举个例子，下图有个 3 层级的跳表。

1748326431445

实际查找示例：
假设要查找「元素：abcd，权重：4」的节点，整个查找过程如下：

第一步：从 L2 层开始

  • 当前位置：头节点的 L2 层
  • 下一个节点：「元素：abc，权重：3」
  • 判断：3 < 4（目标权重），符合条件1，继续在 L2 层前进
  • 到达「元素：abc，权重：3」节点

第二步：继续在 L2 层查找

  • 当前位置：「元素：abc，权重：3」的 L2 层
  • 下一个节点：空节点
  • 判断：下一个节点为空，跳到下一层（L1）

第三步：在 L1 层查找

  • 当前位置：「元素：abc，权重：3」的 L1 层
  • 下一个节点：「元素：abcde，权重：4」
  • 判断：权重相同（4=4），但 “abcde” > “abcd”，不符合条件2，跳到下一层（L0）

第四步：在 L0 层查找

  • 当前位置：「元素：abc，权重：3」的 L0 层
  • 下一个节点：「元素：abcd，权重：4」
  • 判断：找到目标节点！查找结束

这个过程展示了跳表如何利用多层结构快速定位，避免了逐个遍历所有节点。

跳表节点层数设置

层级比例对性能的影响

跳表的性能很大程度上取决于相邻两层节点数量的比例。如果比例不当，查询效率会大打折扣。

不良设计的例子：
下图展示了一个设计不佳的跳表，第二层只有 1 个节点，而第一层有 6 个节点。

1748326449383

问题分析：
如果要查询节点 6，会发生什么？

  • 第二层只能跳到节点 3，然后就没有更多节点了
  • 只能在第一层从节点 3 开始：3→4→5→6，逐个查找
  • 这样就失去了跳表的优势，查询复杂度退化为 O(N)

理想的层级比例：
为了保持跳表的高效性，相邻两层的节点数量最理想的比例是 2:1，这样可以将查找复杂度维持在 O(logN)。

良好设计的例子：
下图展示了一个设计良好的跳表，相邻两层的节点数量比例接近 2:1。

1748326457615

那怎样才能维持相邻两层的节点数量的比例为 2 : 1 呢？

如何维持理想的层级比例？

传统做法是在新增或删除节点时调整跳表结构来维持 2:1 比例，但这会带来额外的计算开销。

Redis 的巧妙解决方案：随机层数生成

Redis 采用了一种更巧妙的方法：在创建节点时随机生成每个节点的层数，而不是严格维持 2:1 比例。

随机生成算法：

  1. 生成一个 [0-1] 范围的随机数
  2. 如果随机数 < 0.25（25% 概率），层数增加 1
  3. 继续生成下一个随机数，重复步骤 2
  4. 直到随机数 ≥ 0.25 为止，确定最终层数

这种方法的特点：

  • 每增加一层的概率是 25%
  • 层数越高，出现概率越低
  • 层高最大限制是 64（Redis 7.0 中是 32）

为什么随机方法有效？

  • 25% 的概率意味着平均每 4 个节点中有 1 个会出现在更高层
  • 这自然形成了接近 4:1 的比例关系（虽然不是严格的 2:1，但仍然有效）
  • 避免了复杂的平衡调整操作

关于头节点的层数：
前面图例中为了简化说明，头节点只画了 3 层，但实际上头节点会直接创建最大层数的结构。如果最大层数限制是 32，那么头节点就有 32 层，这样可以支持任意高度的节点插入。

头节点的创建过程：
从下面的代码可以看到，创建跳表时：

  • 头节点的 level 数组有 ZSKIPLIST_MAXLEVEL 个元素（层）
  • 头节点不存储任何实际数据（member 和 score 都为空）
  • 所有层的 forward 指针都指向 NULL
  • 所有层的 span 值都为 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/* Create a new skiplist. */
zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
}

不同版本的最大层数限制：

  • Redis 7.0：32 层
  • Redis 5.0：64 层
  • Redis 3.0：32 层

可以看到，Redis 在不同版本中对最大层数进行了调整，这是为了在内存使用和性能之间找到更好的平衡点。

为什么用跳表而不用平衡树？

常见面试题解析

这是一个非常经典的面试题：为什么 Zset 选择跳表而不是平衡树（如 AVL 树、红黑树等）？

这个问题，我们可以看看 Redis 作者 @antirez 的原话：

There are a few reasons:

  1. They are not very memory intensive. It’s up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.

  2. A sorted set is often target of many ZRANGE or ZREVRANGE operations, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.

  3. They are simpler to implement, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.

作者观点的总结和深入分析：

作者主要从三个方面说明了选择跳表的原因，让我详细解释一下：

1. 内存使用更灵活

  • 平衡树：每个节点固定包含 2 个指针（左右子树）
  • 跳表：每个节点的指针数量是动态的，平均为 1/(1-p)
  • 在 Redis 中，p=1/4，所以平均每个节点包含 1.33 个指针
  • 结论：跳表比平衡树节省内存

2. 范围查询更简单

  • 平衡树的问题：找到范围的起始值后，需要进行复杂的中序遍历来找到范围内的所有节点
  • 跳表的优势：找到起始值后，只需要在第 1 层（最底层）链表上连续遍历即可
  • 比喻：就像在图书馆找书，跳表相当于找到书架后直接从左到右拿书，而平衡树需要在整个图书馆里按特定顺序跳着找书

3. 实现和维护更简单

  • 平衡树的复杂性：插入和删除可能触发复杂的树结构调整（旋转操作），代码复杂，调试困难
  • 跳表的简单性：插入和删除只需要修改相邻节点的指针，就像在链表中插入节点一样简单
  • 实际好处：代码易读、易维护、易扩展（比如添加 ZRANK 功能只需要少量代码修改）

为什么这些特点对 Redis 很重要？

  • Zset 经常需要范围查询（ZRANGE、ZREVRANGE 等命令）
  • Redis 强调简单和可靠性，复杂的平衡树增加了出错风险
  • 内存是 Redis 的重要考量，跳表的内存效率更符合需求