问题描述
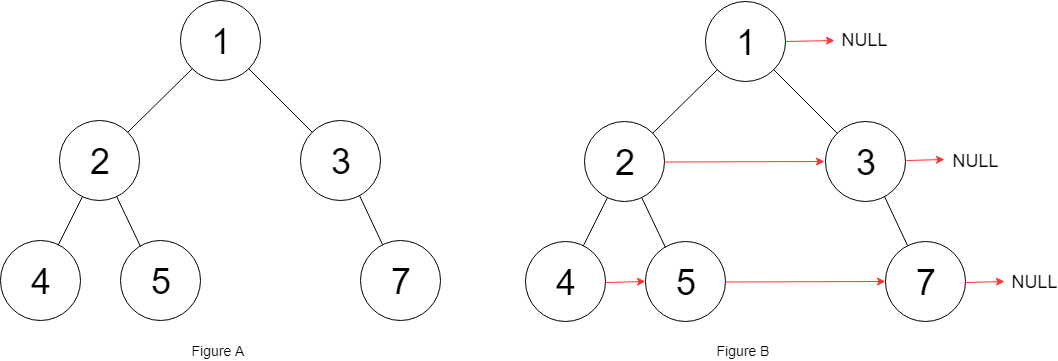
给定一个二叉树，填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。
初始状态下，所有 next 指针都被设置为 NULL。
注意： 这道题与第 116 题的区别在于，这里的二叉树不一定是完美二叉树。
示例
1
2
3
4
5
6
7
8
| 输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
1 → NULL
/ \
2 → 3 → NULL
/ \ \
4→ 5 → 7 → NULL
|
约束条件：
- 树中节点的数量在
[0, 6000] 范围内
-100 <= Node.val <= 100
解题思路
这道题的核心是要为每一层的节点建立从左到右的连接关系。我们需要处理的是一个非完美二叉树，这意味着每层的节点数可能不同，某些节点可能没有左子树或右子树。
关键洞察： 我们需要按层处理节点，将同一层的节点从左到右连接起来。
让我详细介绍三种不同的解法：
解法一：哈希表 + 深度优先搜索（DFS）
核心思想
使用哈希表记录每一层最右侧的节点，通过 DFS 遍历时，如果当前层已经有节点了，就将该节点的 next 指针指向当前节点，然后更新当前层的最右侧节点。
实现细节
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
type Node struct {
Val int
Left *Node
Right *Node
Next *Node
}
func connect(root *Node) *Node {
if root == nil {
return nil
}
levelMap := make(map[int]*Node)
dfs(root, 0, levelMap)
return root
}
func dfs(node *Node, level int, levelMap map[int]*Node) {
if node == nil {
return
}
if prevNode, exists := levelMap[level]; exists {
prevNode.Next = node
}
levelMap[level] = node
dfs(node.Left, level+1, levelMap)
dfs(node.Right, level+1, levelMap)
}
|
执行过程分析
以示例树为例：
1
2
3
4
5
| 1
/ \
2 3
/ \ \
4 5 7
|
- Level 0: 处理节点 1，
levelMap[0] = 1
- Level 1: 处理节点 2，
levelMap[1] = 2；处理节点 3，2.next = 3，levelMap[1] = 3
- Level 2: 处理节点 4，
levelMap[2] = 4；处理节点 5，4.next = 5，levelMap[2] = 5；处理节点 7，5.next = 7，levelMap[2] = 7
解法二：广度优先搜索（BFS）+ 层序遍历
核心思想
使用队列进行层序遍历，逐层处理节点。对于每一层，我们知道该层的节点数量，可以将同一层的节点依次连接起来。
实现细节
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| func connectBFS(root *Node) *Node {
if root == nil {
return nil
}
queue := []*Node{root}
for len(queue) > 0 {
size := len(queue)
for i := 0; i < size; i++ {
node := queue[0]
queue = queue[1:]
if i < size-1 {
node.Next = queue[0]
}
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
}
}
return root
}
|
执行过程分析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| 初始: queue = [1]
第一轮 (Level 0):
- size = 1
- 处理节点 1，queue = [2, 3]
第二轮 (Level 1):
- size = 2
- 处理节点 2，2.next = 3，queue = [3, 4, 5]
- 处理节点 3，queue = [4, 5, 7]
第三轮 (Level 2):
- size = 3
- 处理节点 4，4.next = 5，queue = [5, 7]
- 处理节点 5，5.next = 7，queue = [7]
- 处理节点 7，queue = []
|
解法三：O(1) 空间复杂度优化
核心思想
利用已经建立的 next 指针来遍历下一层，不使用额外的数据结构。我们维护两个指针：
levelStart: 当前层的起始节点prev: 下一层的前一个节点
实现细节
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| func connectOptimized(root *Node) *Node {
if root == nil {
return nil
}
levelStart := root
for levelStart != nil {
var prev *Node
var nextStart *Node
for node := levelStart; node != nil; node = node.Next {
if node.Left != nil {
if prev != nil {
prev.Next = node.Left
} else {
nextStart = node.Left
}
prev = node.Left
}
if node.Right != nil {
if prev != nil {
prev.Next = node.Right
} else {
nextStart = node.Right
}
prev = node.Right
}
}
levelStart = nextStart
}
return root
}
|
方法比较
| 方面 |
哈希表 DFS |
队列 BFS |
O(1) 空间优化 |
| 时间复杂度 |
O(n) |
O(n) |
O(n) |
| 空间复杂度 |
O(n) |
O(n) |
O(1) |
| 优点 |
实现简单，易理解 |
层次清晰，符合直觉 |
空间效率最高 |
| 缺点 |
需要额外哈希表 |
需要队列存储 |
实现复杂，理解难度大 |
| 推荐度 |
★★★☆☆ |
★★★★☆ |
★★★★★ |
复杂度分析
时间复杂度
所有三种方法的时间复杂度都是 O(n)，其中 n 是树中节点的数量。我们需要访问每个节点恰好一次。
空间复杂度
- 哈希表 DFS: O(n)，最坏情况下哈希表需要存储所有层的信息
- 队列 BFS: O(n)，最坏情况下队列需要存储最底层的所有节点
- O(1) 优化: O(1)，只使用常数额外空间
关键收获
- 层序遍历的两种实现方式：队列 BFS 和利用已建立的 next 指针
- 空间优化技巧：利用问题的特殊性质（next 指针）来避免使用额外数据结构
- DFS vs BFS：对于树的层次处理，BFS 通常更直观，但 DFS 配合哈希表也能解决
- 常见陷阱：
- 忘记处理空节点的情况
- 在 O(1) 解法中，容易搞混当前层和下一层的指针关系
- DFS 时要注意遍历顺序（先左后右）
这道题是一个很好的练习，展示了如何用不同的思路解决同一个问题，以及如何在保持正确性的前提下优化空间复杂度。