LeetCode 222 - 完全二叉树的节点个数（Count Complete Tree Nodes）

问题描述

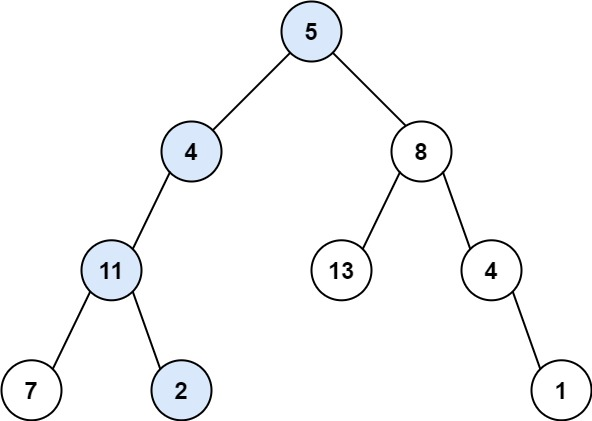
给你一棵完全二叉树的根节点 root，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最底层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1 ~ 2^(h-1) 个节点。

示例 1：

1 2	输入：root = [1,2,3,4,5,6] 输出：6

示例 2：

1 2	输入：root = [] 输出：0

示例 3：

1 2	输入：root = [1] 输出：1

约束条件：

树中节点的数目范围是 [0, 5 * 10^4]
0 <= Node.val <= 5 * 10^4
题目数据保证输入的树是完全二叉树

解题思路

这道题的关键在于利用完全二叉树的性质来优化计算。

如果直接遍历整个树来计算节点个数，时间复杂度会是 O(n)。但是，完全二叉树有一个重要性质：对于完全二叉树的任意子树，如果其左子树的高度等于右子树的高度，那么这个子树是一个满二叉树。

核心思想

满二叉树的节点个数：对于高度为 h 的满二叉树，节点个数为 $2^h - 1$
高度计算：通过计算左子树的高度（一直往左走）和右子树的高度（一直往右走）
递归判断：
- 如果左子树高度 = 右子树高度 → 满二叉树 → 使用公式计算
- 如果左子树高度 ≠ 右子树高度 → 递归计算左右子树 + 根节点

算法步骤

边界条件：如果节点为空，返回 0
计算高度：
- 从当前节点开始，一直向左走，计算左子树高度 hl
- 从当前节点开始，一直向右走，计算右子树高度 hr
判断是否为满二叉树：
- 如果 hl == hr，说明是满二叉树，返回 $2^{hl} - 1$
- 如果 hl != hr，递归计算：countNodes(left) + 1 + countNodes(right)

为什么这样做是正确的？

对于完全二叉树，如果左子树高度等于右子树高度，说明左子树是满的，右子树也是满的（除了可能最后一层）。但由于我们计算的是从根到最深叶子的路径长度，如果左右路径长度相等，说明整个子树都是满的。

代码实现

func countNodes(root *TreeNode) int {
    if root == nil {
        return 0
    }
    
    var dfs func(node *TreeNode) int
    dfs = func(node *TreeNode) int {
        if node == nil {
            return 0
        }
        
        // 计算左子树高度
        hl := 0
        cur := node
        for cur != nil {
            cur = cur.Left
            hl++
        }
        
        // 计算右子树高度
        hr := 0
        cur = node
        for cur != nil {
            cur = cur.Right
            hr++
        }
        
        // 如果高度相等，说明是满二叉树
        if hl == hr {
            return 1<<hl - 1  // 等价于 2^hl - 1
        }
        
        // 否则递归计算左右子树
        return dfs(node.Left) + 1 + dfs(node.Right)
    }
    
    return dfs(root)
}

关键实现细节

高度计算：从当前节点开始计算，所以根节点的高度为 1
位运算优化：1<<hl - 1 等价于 $2^{hl} - 1$，利用位运算提高效率
递归结构：使用内部函数 dfs 来实现递归逻辑

复杂度分析

时间复杂度：$O(\log^2 n)$

推导过程：

每次递归调用时，我们需要计算左右子树的高度，这需要 $O(\log n)$ 时间
在最坏情况下，我们需要递归 $O(\log n)$ 次（树的高度）
因此总时间复杂度为 $O(\log n \times \log n) = O(\log^2 n)$

为什么不是 O(n)？

关键在于我们不是每个节点都访问
每次递归时，要么直接计算出满二叉树的节点数，要么只递归到一个子树
这大大减少了需要访问的节点数量

空间复杂度：$O(\log n)$

递归调用栈的深度最多为树的高度
完全二叉树的高度为 $O(\log n)$

方法比较

方面	暴力遍历	本题解法
时间复杂度	$O(n)$	$O(\log^2 n)$
空间复杂度	$O(\log n)$	$O(\log n)$
优点	思路简单直接	充分利用完全二叉树性质
缺点	没有利用题目条件	实现相对复杂
推荐度	★★★☆☆	★★★★★

关键收获

利用数据结构特性：完全二叉树的特殊性质是解决这个问题的关键
满二叉树判断：通过比较左右子树高度来判断是否为满二叉树
递归优化：不是所有子树都需要递归，大大提高了效率
位运算应用：使用 1<<h 代替 pow(2,h) 提高计算效率

常见陷阱

高度计算错误：注意从当前节点开始计算高度，根节点高度为 1
公式记忆错误：满二叉树节点数是 $2^h - 1$，不是 $2^h$
递归终止条件：要正确处理空节点的情况

Adrian Wang's blog