LeetCode 133 - 克隆图（Clone Graph）

问题描述

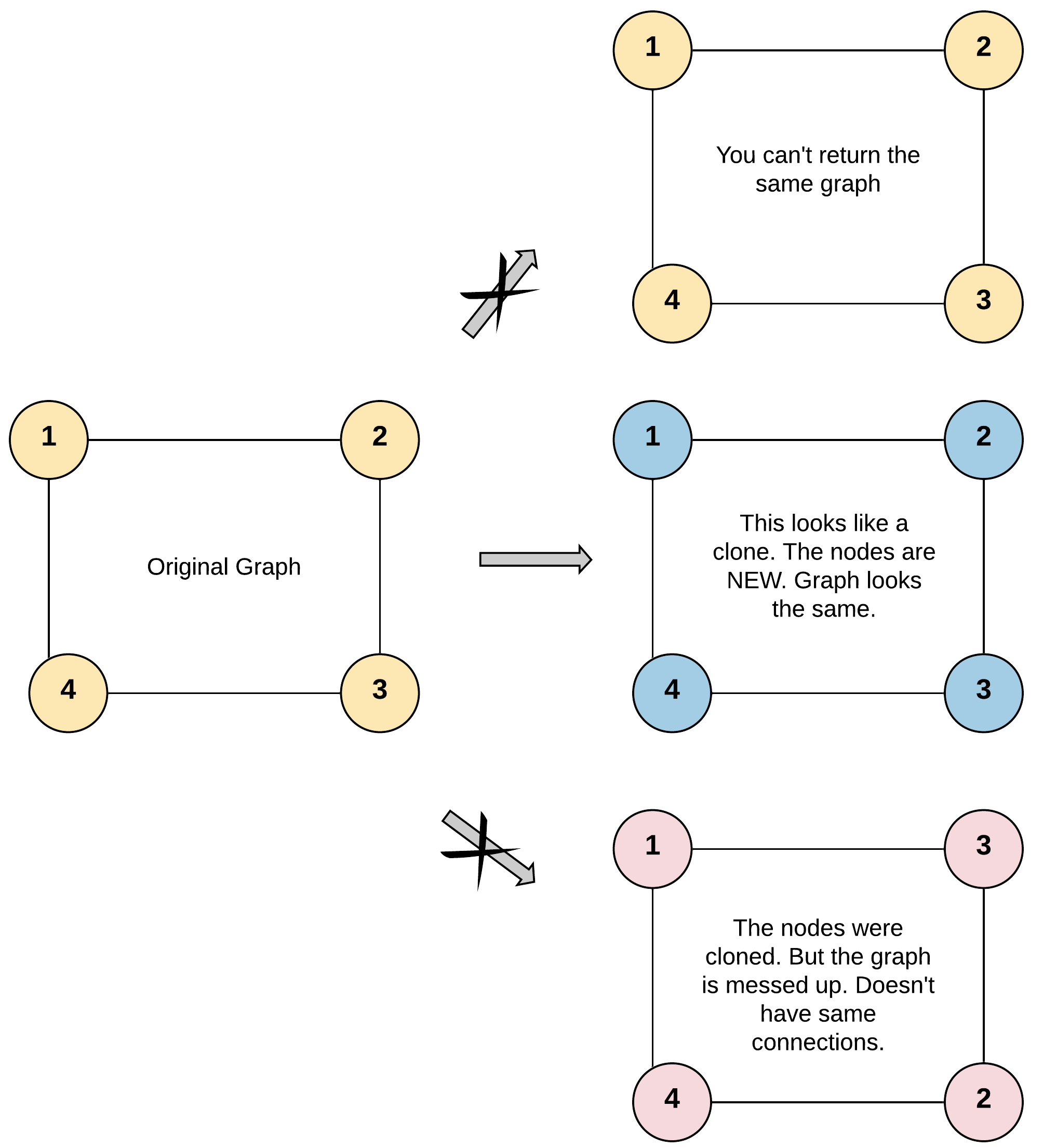
给你无向连通图中一个节点的引用，请你返回该图的深拷贝（克隆）。

图中的每个节点都包含它的值 val（int）和其邻居的列表（list[Node]）。

class Node {
    public int val;
    public List<Node> neighbors;
}

测试用例格式

简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1（val = 1），第二个节点值为 2（val = 2），以此类推。该图在测试用例中使用邻接列表表示。

邻接列表是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。

给定节点将始终是图中的第一个节点（值为 1）。你必须将给定节点的拷贝作为对克隆图的引用返回。

示例

示例 1：

输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
输出：[[2,4],[1,3],[2,4],[1,3]]
解释：
图中有 4 个节点。
节点 1 的值是 1，它有两个邻居：节点 2 和节点 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和节点 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和节点 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和节点 3 。

示例 2：

1
2
3

输入：adjList = [[]]
输出：[[]]
解释：输入包含一个空列表。该图仅仅只有一个值为 1 的节点，它没有任何邻居。

示例 3：

1
2
3

输入：adjList = []
输出：[]
解释：这个图是空的，它不含任何节点。

约束条件

节点数不超过 100
1 <= Node.val <= 100
每个节点值 Node.val 都是唯一的
无向图
图是连通的，你可以从给定节点访问到所有节点

解题思路

这是一个图的深拷贝问题，核心挑战在于处理图中的环形引用。如果直接递归复制，会陷入无限循环。

核心思路

使用深度优先搜索（DFS）+ 哈希表来解决：

哈希表记录映射关系：用 visited 哈希表记录原节点到克隆节点的映射关系
避免重复访问：如果节点已经被访问过，直接返回对应的克隆节点
递归构建邻居关系：对每个邻居节点递归调用克隆函数

关键洞察

访问标记的时机至关重要：必须在开始处理邻居之前就建立原节点到克隆节点的映射关系，而不是在处理完邻居之后。这样可以避免在处理环形引用时出现无限递归。

实现细节

算法步骤

边界处理：如果输入节点为空，直接返回 nil
检查是否已访问：如果当前节点已经在 visited 中，说明已经克隆过，直接返回克隆节点
创建克隆节点：创建一个新节点，值与原节点相同，邻居列表为空
⭐ 关键步骤：立即将原节点和克隆节点的映射关系存入 visited
递归处理邻居：遍历原节点的所有邻居，递归调用克隆函数，将返回的克隆邻居添加到当前克隆节点的邻居列表中
返回克隆节点

为什么要先建立映射关系？

考虑这样的图结构：

1 ---- 2
|      |
|      |
4 ---- 3

如果我们在处理完邻居后才建立映射：

克隆节点 1，开始处理其邻居节点 2 和 4
递归克隆节点 2，开始处理其邻居节点 1 和 3
递归克隆节点 1（又回到了节点 1！）
因为节点 1 还没有在 visited 中建立映射，会重新开始克隆过程
无限递归！

代码实现

正确实现

func cloneGraph(node *Node) *Node {
    visited := map[*Node]*Node{}
    
    var dfs func(cur *Node) *Node
    
    dfs = func(cur *Node) *Node {
        // 边界条件
        if cur == nil {
            return cur
        }
        
        // 如果已经访问过，直接返回克隆节点
        if clonedNode, ok := visited[cur]; ok {
            return clonedNode
        }
        
        // 创建克隆节点
        clonedNode := &Node{cur.Val, []*Node{}}
        
        // ⭐ 关键：立即建立映射关系！
        visited[cur] = clonedNode
        
        // 递归处理所有邻居
        for _, neighbor := range cur.Neighbors {
            clonedNode.Neighbors = append(clonedNode.Neighbors, dfs(neighbor))
        }
        
        return clonedNode
    }
    
    return dfs(node)
}

错误实现分析

❌ 错误的代码（将 visited[cur] = clonedNode 放在最后）：

func cloneGraph(node *Node) *Node {
    visited := map[*Node]*Node{}
    
    var dfs func(cur *Node) *Node
    
    dfs = func(cur *Node) *Node {
        if cur == nil {
            return cur
        }
        
        if clonedNode, ok := visited[cur]; ok {
            return clonedNode
        }
        
        clonedNode := &Node{cur.Val, []*Node{}}
        
        // 递归处理所有邻居
        for _, neighbor := range cur.Neighbors {
            clonedNode.Neighbors = append(clonedNode.Neighbors, dfs(neighbor))
        }
        
        // ❌ 错误：太晚建立映射关系！
        visited[cur] = clonedNode
        
        return clonedNode
    }
    
    return dfs(node)
}

错误原因详细分析

问题根源

时机错误：在处理邻居的递归调用过程中，当前节点还没有被标记为"已访问"，导致在环形引用的情况下会重复进入同一个节点。

具体执行过程

以图 1-2-1 为例（节点 1 和节点 2 互相连接）：

第一次调用 dfs(node1)：
- visited 为空，创建 clonedNode1
- 开始处理 node1 的邻居 node2
- 调用 dfs(node2)
第二次调用 dfs(node2)：
- visited 仍为空（node1 还没被添加），创建 clonedNode2
- 开始处理 node2 的邻居 node1
- 调用 dfs(node1) ← 又回到了节点 1！
第三次调用 dfs(node1)：
- visited 仍为空，再次创建新的 clonedNode1
- 开始处理邻居…
- 无限递归开始！

Runtime Error 的具体表现

Stack Overflow：递归栈深度超出限制
超时错误：程序陷入无限循环
内存溢出：不断创建新的节点对象

复杂度分析

时间复杂度：$O(N + M)$

$N$ 是节点数量，$M$ 是边的数量
每个节点访问一次：$O(N)$
每条边访问一次：$O(M)$

空间复杂度：$O(N)$

visited 哈希表存储：$O(N)$
递归调用栈深度：$O(N)$（最坏情况下是链状图）
克隆图的存储空间：$O(N + M)$（不计入结果空间）

方法比较

方面	正确实现	错误实现
映射建立时机	创建节点后立即建立	处理完邻居后建立
环形引用处理	✅ 正确处理	❌ 无限递归
时间复杂度	$O(N + M)$	无法完成（超时/栈溢出）
空间复杂度	$O(N)$	无法完成（内存溢出）
运行结果	✅ 通过所有测试用例	❌ Runtime Error

关键收获

重要概念

图的深拷贝：不仅要复制节点值，还要正确复制节点间的连接关系
环形引用检测：使用哈希表记录访问状态，避免重复访问
访问标记时机：在开始处理当前节点时就要标记，而不是处理完成后

常见陷阱

❌ 访问标记时机错误：在递归处理邻居之后才标记访问状态
❌ 忘记处理空图：没有检查输入节点是否为 nil
❌ 邻居列表初始化错误：没有正确初始化克隆节点的邻居列表

实际应用

对象深拷贝：在需要完全独立的对象副本时
图数据库：复制图结构用于备份或分析
社交网络：复制用户关系网络的子图

这道题的核心教训是：在处理有环数据结构时，访问标记的时机至关重要。必须在开始处理当前元素时就进行标记，而不是等处理完成后再标记。这是避免无限递归的关键！

Adrian Wang's blog