问题描述
给你一个大小为 n x n 的整数矩阵 board,其中 n 和 board[i][j] 都在范围 [1, n] 内。
蛇梯棋的棋盘上标有从 1 到 n² 的数字,按从左到右,从下到上的 蛇形 方式编号。
玩家从棋盘上的方格 1 (总是在最后一行、第一列)开始出发。
每一回合,玩家都要从当前方格开始出发,按以下规则前进:
- 选择目标方格来决定下一步的移动,目标方格的编号是
[curr + 1, curr + 6] 的范围内任意整数 curr 是玩家当前所在的方格编号。
- 该选择模拟了掷 六面骰子 的情景,无论棋盘大小如何,玩家最多只能有 6 个目的地。
- 如果目标方格有蛇或梯子,玩家必须按蛇梯的指示前进。蛇梯的目的地不会有蛇或梯子。
- 注意,玩家在每回合的移动过程中最多只能爬过蛇或梯子一次:就算目的地是另一条蛇或梯子的起点,玩家也不能继续移动。
返回达到编号为 n² 的方格所需的最少移动次数,如果不可能,则返回 -1。
示例 1:
1
2
3
4
5
6
7
8
9
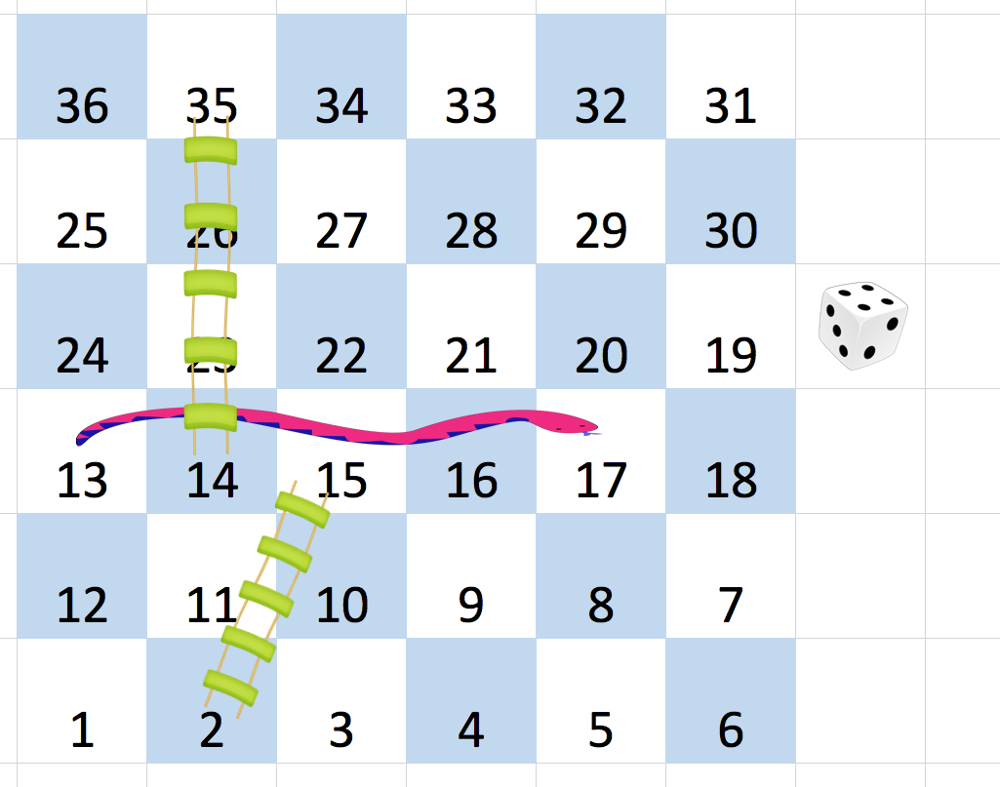
| 输入:board = [[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,35,-1,-1,13,-1],[-1,-1,-1,-1,-1,-1],[-1,15,-1,-1,-1,-1]]
输出:4
解释:
首先,从方格 1 [第 5 行,第 0 列] 开始。
决定移动到方格 2,并必须爬过梯子移动到方格 15。
然后决定移动到方格 17 [第 3 行,第 5 列],必须爬过蛇到方格 13。
接下来决定移动到方格 14,且必须爬过梯子移动到方格 35。
最后决定移动到方格 36 [第 0 行,第 5 列],游戏结束。
可以证明需要至少 4 次移动才能到达最后一个方格,所以答案是 4。
|

示例 2:
1
2
| 输入:board = [[-1,-1],[-1,3]]
输出:1
|
❌ 错误分析过程
遇到的主要问题
1. 内存限制超出 (Memory Limit Exceeded)
错误现象:
1
2
3
4
| Memory Limit Exceeded
5/217 cases passed (N/A)
Testcase: [[-1,4,-1],[6,2,6],[-1,3,-1]]
Expected Answer: 2
|
分析: 这个错误是由于存在循环蛇梯导致的无限递归调用。在测试案例中:
形成了循环,numToNode 函数会无限递归调用自己,导致栈溢出。
2. 坐标转换逻辑复杂
蛇梯棋的编号规则相当复杂:
- 从棋盘底部开始编号(1 在最后一行第一列)
- 奇数行从左到右,偶数行从右到左
- 需要正确处理数组索引到棋盘编号的转换
多次尝试的坐标转换方案:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
if row%2 == 0 && n%2 == 0 {
col = n - 1 - col
}
if (n-1-row)%2 == 1 {
col = n - 1 - col
}
row := (num - 1) / n
if row%2 == 1 {
col = n - 1 - col
}
row = n - 1 - row
|
3. BFS 访问控制问题
问题: 没有正确处理已访问节点的标记,导致:
4. 递归vs迭代的选择
最初使用递归的 numToNode 函数来处理蛇梯跳转,但遇到循环蛇梯时会导致栈溢出。
解题思路分析
核心算法: BFS (广度优先搜索)
这是一个典型的最短路径问题,应该使用 BFS 来解决:
- 状态表示: 每个状态包含当前位置编号和步数
- 状态转移: 从当前位置可以移动到
[curr+1, curr+6] 范围内的任意位置
- 蛇梯处理: 如果到达的位置有蛇或梯子,需要跳转到指定位置
- 终止条件: 到达编号为
n² 的位置
关键难点
1. 坐标转换
1
2
3
4
5
6
7
8
9
10
11
| 棋盘编号示例 (4x4):
13 14 15 16
12 11 10 9
5 6 7 8
4 3 2 1
对应数组索引:
[0,0] [0,1] [0,2] [0,3]
[1,0] [1,1] [1,2] [1,3]
[2,0] [2,1] [2,2] [2,3]
[3,0] [3,1] [3,2] [3,3]
|
2. 蛇梯处理
- 需要在到达新位置后立即检查是否有蛇或梯子
- 避免无限递归调用
- 正确处理循环蛇梯的情况
3. 访问控制
- 使用
visited 数组避免重复访问
- 注意数组索引范围(编号1到n²)
错误代码实现历程
第一版:最初的错误实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| package main
import "fmt"
type Location struct {
X int
Y int
step int
Num int
}
func snakesAndLadders(board [][]int) int {
n := len(board)
var numToNode func(num int) Location
numToNode = func(num int) Location {
row := n - 1 - (num-1)/n
col := (num - 1) % n
if row%2 == 0 && n%2 == 0 {
col = n - 1 - col
}
if board[row][col] >= 0 {
return numToNode(board[row][col])
}
return Location{X: row, Y: col, step: 0, Num: num}
}
start := numToNode(1)
fmt.Println(start)
end := numToNode(n * n)
cnt := 0
queue := []Location{start}
for len(queue) != 0 && cnt <= n*n {
top := queue[0]
queue = queue[1:]
cnt++
if top.X == end.X && top.Y == end.Y {
return top.step
}
if board[top.X][top.Y] == -2 {
continue
}
board[top.X][top.Y] = -2
for i := 1; i <= 6; i++ {
if top.Num+i <= n*n {
next := numToNode(top.Num + i)
next.step = top.step + 1
queue = append(queue, next)
}
}
}
return -1
}
|
问题分析:
- 坐标转换条件
row%2 == 0 && n%2 == 0 完全错误
- 使用递归的
numToNode 函数处理蛇梯跳转,遇到循环时会栈溢出
- 用修改原数组的方式标记访问,不够优雅且容易出错
- 终止条件用坐标比较,不如直接用编号比较
第二版:尝试修复坐标转换和访问控制
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| func snakesAndLadders(board [][]int) int {
n := len(board)
visited := make([]bool, n*n+1)
var numToNode func(num int) Location
numToNode = func(num int) Location {
row := n - 1 - (num-1)/n
col := (num - 1) % n
if (n-1-row)%2 == 1 {
col = n - 1 - col
}
if board[row][col] != -1 {
return numToNode(board[row][col])
}
return Location{X: row, Y: col, step: 0, Num: num}
}
start := numToNode(1)
start.step = 0
queue := []Location{start}
visited[1] = true
for len(queue) != 0 {
top := queue[0]
queue = queue[1:]
if top.Num == n*n {
return top.step
}
for i := 1; i <= 6; i++ {
nextNum := top.Num + i
if nextNum <= n*n && !visited[nextNum] {
next := numToNode(nextNum)
next.step = top.step + 1
visited[nextNum] = true
queue = append(queue, next)
}
}
}
return -1
}
|
问题分析:
- ✅ 修正了坐标转换逻辑
- ✅ 使用了proper的visited数组
- ✅ 修正了终止条件
- ❌ 仍然使用递归处理蛇梯,循环蛇梯时会导致栈溢出
第三版:最终尝试的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| func snakesAndLadders(board [][]int) int {
n := len(board)
var numToNode func(num int) Location
numToNode = func(num int) Location {
row := (num - 1) / n
col := (num - 1) % n
if row%2 == 1 {
col = n - 1 - col
}
row = n - 1 - row
return Location{X: row, Y: col, step: 0, Num: num}
}
start := numToNode(1)
visited := make([]bool, n*n)
queue := []Location{start}
for len(queue) != 0 {
top := queue[0]
queue = queue[1:]
for i := 1; i <= 6; i++ {
if top.Num+i > n*n {
break
}
next := numToNode(top.Num + i)
if board[next.X][next.Y] > 0 {
next = numToNode(board[next.X][next.Y])
}
if next.Num == n*n {
return top.step + 1
}
if visited[next.Num] {
continue
}
visited[next.Num] = true
next.step = top.step + 1
queue = append(queue, next)
}
}
return -1
}
|
问题分析:
- visited数组越界:
visited := make([]bool, n*n) 长度为nn,但编号范围是[1,nn],访问 visited[n*n] 会越界
- 递归问题未解决: 仍然使用递归处理蛇梯跳转
- 坐标转换逻辑: 多次修改,但仍不确定正确性
正确解题思路分析
1. 坐标转换的正确逻辑
蛇梯棋的编号规则需要仔细理解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| 6x6棋盘编号示例:
31 32 33 34 35 36
30 29 28 27 26 25
19 20 21 22 23 24
18 17 16 15 14 13
7 8 9 10 11 12
6 5 4 3 2 1
对应数组索引:
[0,0][0,1][0,2][0,3][0,4][0,5]
[1,0][1,1][1,2][1,3][1,4][1,5]
[2,0][2,1][2,2][2,3][2,4][2,5]
[3,0][3,1][3,2][3,3][3,4][3,5]
[4,0][4,1][4,2][4,3][4,4][4,5]
[5,0][5,1][5,2][5,3][5,4][5,5]
|
正确的坐标转换公式:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| func numToPos(num, n int) (int, int) {
bottomRow := (num - 1) / n
row := n - 1 - bottomRow
col := (num - 1) % n
if bottomRow%2 == 1 {
col = n - 1 - col
}
return row, col
}
|
关键理解:
bottomRow = (num-1) / n 计算从底部数的行号- 从底部数的奇数行(bottomRow=0,2,4…):从左到右
- 从底部数的偶数行(bottomRow=1,3,5…):从右到左
2. 避免递归的蛇梯处理
错误方式(会导致栈溢出):
1
2
3
4
5
6
7
| func numToNode(num int) Location {
row, col := numToPos(num, n)
if board[row][col] != -1 {
return numToNode(board[row][col])
}
return Location{X: row, Y: col, Num: num}
}
|
正确方式(在BFS中直接处理):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
nextNum := curr.Num + i
row, col := numToPos(nextNum, n)
if board[row][col] != -1 {
nextNum = board[row][col]
}
if !visited[nextNum] {
visited[nextNum] = true
newRow, newCol := numToPos(nextNum, n)
queue = append(queue, Location{X: newRow, Y: newCol, Num: nextNum, step: curr.step + 1})
}
|
3. 完整的正确实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| type Location struct {
X int
Y int
step int
Num int
}
func snakesAndLadders(board [][]int) int {
n := len(board)
numToPos := func(num int) (int, int) {
bottomRow := (num - 1) / n
row := n - 1 - bottomRow
col := (num - 1) % n
if bottomRow%2 == 1 {
col = n - 1 - col
}
return row, col
}
visited := make([]bool, n*n+1)
queue := []Location{{Num: 1, step: 0}}
visited[1] = true
for len(queue) > 0 {
curr := queue[0]
queue = queue[1:]
if curr.Num == n*n {
return curr.step
}
for dice := 1; dice <= 6; dice++ {
nextNum := curr.Num + dice
if nextNum > n*n {
break
}
row, col := numToPos(nextNum)
if board[row][col] != -1 {
nextNum = board[row][col]
}
if !visited[nextNum] {
visited[nextNum] = true
finalRow, finalCol := numToPos(nextNum)
queue = append(queue, Location{
X: finalRow,
Y: finalCol,
Num: nextNum,
step: curr.step + 1,
})
}
}
}
return -1
}
|
4. 关键技术要点
A. 坐标转换的数学原理
1
2
3
4
5
6
7
8
9
10
|
bottomRow := (num - 1) / n
col := (num - 1) % n
if bottomRow%2 == 1 {
col = n - 1 - col
}
row := n - 1 - bottomRow
|
B. 循环蛇梯的处理
- 关键思想: 在BFS中直接处理跳转,不使用递归
- 访问标记: 对最终到达的位置进行标记,避免重复访问
- 一次跳转: 题目保证蛇梯的目的地不会再有蛇梯
C. BFS的优化要点
1
2
3
4
5
6
7
8
9
10
11
12
|
visited := make([]bool, n*n+1)
if nextNum > n*n {
break
}
if curr.Num == n*n {
return curr.step
}
|
5. 复杂度分析
-
时间复杂度: O(n²)
-
空间复杂度: O(n²)
- visited数组: O(n²)
- BFS队列: 最坏情况O(n²)
仍存在的问题
1. visited数组索引越界
1
2
| visited := make([]bool, n*n)
|
2. 递归问题未解决
仍然使用 numToNode 递归函数,遇到循环蛇梯时依然会有问题。
3. 坐标转换的正确性
多次修改坐标转换逻辑,但仍不确定是否完全正确。
关键收获与反思
算法层面
- BFS是正确的选择: 求最短路径问题应该使用BFS
- 状态设计要清晰: 明确每个状态包含的信息
- 边界条件要仔细: 数组索引、编号范围等细节很重要
实现层面
- 坐标转换是核心难点: 蛇梯棋的编号规则比较复杂
- 递归vs迭代要权衡: 对于可能有循环的场景,迭代更安全
- 访问控制必不可少: 避免重复访问和无限循环
调试技巧
- 小数据测试: 用简单的测试案例验证坐标转换逻辑
- 边界条件检查: 特别关注数组越界问题
- 循环检测: 对于图相关问题要考虑循环的处理
错误根因总结
通过深入分析,这道题的错误主要集中在以下几个方面:
1. 坐标转换理解不够深入
- 错误: 多次尝试不同的转换公式,但都没有正确理解蛇形编号的数学规律
- 正确: 需要清楚理解
bottomRow = (num-1)/n 和翻转条件 bottomRow%2 == 1
2. 递归vs迭代的选择失误
- 错误: 使用递归处理蛇梯跳转,遇到循环时导致栈溢出
- 正确: 在BFS主循环中直接处理跳转,避免函数调用栈问题
3. 边界条件处理不当
- 错误: visited数组长度为nn,但编号范围是[1,nn],导致越界
- 正确: visited数组长度应为nn+1,或者将编号映射到[0,nn-1]范围
4. 访问控制时机错误
- 错误: 在出队时才标记访问,或者标记时机不当
- 正确: 在入队时立即标记最终位置为已访问
算法学习收获
技术层面
-
坐标转换公式推导:
- 理解二维编号到一维数组的映射关系
- 掌握蛇形路径的数学规律
-
BFS实现技巧:
- 合理的visited数组设计
- 正确的访问标记时机
- 边界条件的全面检查
-
避免递归陷阱:
- 识别可能存在循环的场景
- 选择迭代而非递归的处理方式
思维层面
- 问题分解能力: 将复杂问题拆分为坐标转换、蛇梯处理、BFS遍历等子问题
- 边界意识: 时刻关注数组索引范围、编号范围等边界条件
- 调试思维: 通过具体例子验证算法逻辑的正确性
代码质量
- 函数设计: 将坐标转换抽象为独立函数,提高代码可读性
- 变量命名: 使用有意义的变量名(如bottomRow)帮助理解
- 注释习惯: 在关键逻辑处添加说明,特别是数学公式部分
总结
LeetCode 909 蛇梯棋是一道综合性很强的题目,涉及:
- 图论: BFS最短路径
- 数学: 坐标转换公式推导
- 编程技巧: 避免递归、正确的访问控制
核心教训:
- 理论先行: 在编码前要完全理解问题的数学模型
- 细节关键: 边界条件、数组索引等细节往往决定成败
- 迭代优于递归: 对于可能有循环的图问题,优先考虑迭代解法
- 测试验证: 用简单例子验证关键逻辑(如坐标转换)的正确性
标记为错题的价值: 通过完整记录错误过程和正确思路,为今后遇到类似的坐标转换、BFS遍历问题提供了宝贵的参考经验。这种深度分析比简单的AC更有学习价值。